Să aprofundăm în conceptele de putere CA, cum să calculăm puterea instantanee, puterea medie, puterea reactivă, puterea complexă și factorul de putere. Vom vorbi și despre relația pe care fiecare concept o are între ele.

Puterea instantanee

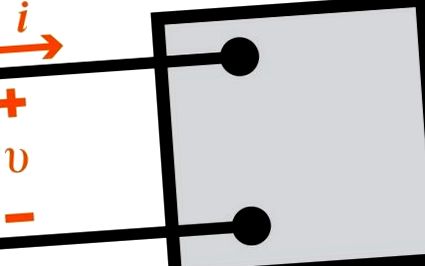
Începem explorarea calculelor puterii sinusoidale cu circuitul genaric din Fig. 1.1. Aici, v și eu sunt semnale sinusoidale stabile. Prin utilizarea convenției semnelor pasive (PSC), puterea în orice moment este dată de:

articole

Figura 1.1 Reprezentarea unui circuit utilizat pentru calcularea puterii.

Ecuația 1.1 descrie puterea instantanee. Amintiți-vă că, dacă direcția de referință a curentului este în direcția creșterii tensiunii, Eq. 1.1 trebuie scris cu un semn minus. Puterea instantanee este întotdeauna măsurată în wați atunci când tensiunea este măsurată în volți și curentul este măsurat în amperi. Două expresii ale unghiurilor de fază ale v și eu sunt scrise ca

$$ v = V_ \ cos (\ omega t + \ theta _), $$ (1.2)

$$ i = I_ \ cos (\ omega t + \ theta _), $$ (1,3)

În aceste două expresii, $$ \ theta _ $$ este unghiul de fază al tensiunii și $$ \ theta _$$ este unghiul de fază actual.

În timp ce se lucrează în stare de echilibru sinusoidală, poate fi aleasă o referință convenabilă pentru timp zero. Inginerilor care proiectează sisteme care transferă cantități mari de energie le-a fost convenabil să folosească un timp zero care corespunde curentului instantaneu care trece printr-un maxim pozitiv. Alegând un astfel de timp de referință, o schimbare atât a tensiunii, cât și a curentului cu $$ \ theta _$$ este obligatoriu. Acum, ec. 1.2 și 1.3 devin

$$ v = V_ \ cos (\ omega t + \ theta _ - \ theta _) $$ (1,4)

$$ i = I_ \ cos (\ omega t) $$ (1,5)

Dacă ecv. 1.4 și 1.5 sunt substituite în ecuație. 1.1, expresia puterii instantanee devine acum

$$ p = V_I_ \ cos (\ omega t + \ theta _ - \ theta _) \ cos (\ omega t) $$ (1,6)

Eq. 1.6 poate fi folosit pentru a rezolva puterea medie așa cum este; totuși, aplicând câteva identități trigonometrice simple, ecuația puterii instantanee poate fi simplificată. Utilizarea identității produsului cosinusului dă

$$ \ cos (\ alpha) \ cos (\ beta) = \ frac \ cos (\ alpha - \ beta) + \ frac \ cos (\ alpha + \ beta) $$

Leasing $$ \ alpha = \ omega t + \ theta _- \ theta _$$ și $$ \ beta = \ omega t $$ oferă

$$ p = \ fracI _> \ cos (\ theta _- \ theta _) + \ fracI _> \ cos [2 \ omega t + \ theta _- \ theta _) $$ (1,7)

În cele din urmă, folosind identitatea cosumului unghi-sumă

$$ \ cos (\ alpha + \ beta) = \ cos (\ alpha) \ cos (\ beta) - \ sin (\ alpha) \ sin (\ beta) $$

pentru a extinde al doilea termen pe partea dreaptă a ecuației 1.7, care dă

$$ p = \ frac >> \ cos (\ theta _- \ theta _) + \ fracI _> \ cos \ \ theta _- \ theta _) \ cos (2 \ omega t) - \ fracI _> \ sin (\ theta _- \ theta _) \ sin (2 \ omega t) $$ (1,8)

Relația dintre curent, putere și tensiune

Figura 1.2 de mai jos prezintă relația dintre eu, v, și p, presupunând că $$ \ theta _ = 60 ^ $$ și $$ \ theta _= 0 ^ $$. Frecvența puterii instantanee este de două ori frecvența curentului sau a tensiunii. Această descriere urmează și din cei doi termeni din partea dreaptă a ecuației. 1.8. Aceasta înseamnă că puterea instantanee trece prin două cicluri complete pentru fiecare ciclu al curentului sau al tensiunii. Dacă te uiți la Fig. 1.2, puterea instantanee poate fi negativă pentru o porțiune a fiecărui ciclu, chiar dacă rețeaua dintre terminale este pasivă. Într-o rețea pasivă, această putere negativă implică faptul că energia stocată în inductoare sau condensatoare este acum extrasă. În timp ce puterea instantanee variază în funcție de timp în starea de echilibru sinusoidală a unui circuit, aceasta provoacă unele vibrații în unele aparate acționate de motor. Datorită acestei vibrații în aceste aparate, sunt necesare suporturi rezistente ale motorului pentru a reduce orice vibrație excesivă.

Figura 1.2 Puterea, curentul și tensiunea instantanee vs. frecvența unghiulară

Puterea medie și reactivă

Eq. 1.8 poate fi acum utilizat pentru a găsi puterea medie la bornele circuitului, precum și pentru a stabili conceptul de putere reactivă. Observând că ecuația are trei termeni, poate fi rescrisă ca

$$ p = P + P \ cos (2 \ omega t) -Q \ sin (2 \ omega t), $$ (1,9)

Puterea medie (reală) $$ P = \ fracI _> \ cos (\ theta _- \ theta _) $$ (1,10)

Puterea reactivă $$ Q = \ fracI _> \ sin (\ theta _- \ theta _) $ $ (1,11)

P se numește putere medie, iar Q se numește putere reactivă. Puterea medie este, de asemenea, cunoscută sub numele de putere reală, deoarece este puterea reală într-un circuit care este transformat din energie electrică în energie neelectrică. Puterea medie asociată cu semnalele sinusoidale este media puterii instantanee pe o perioadă sau

Unde T este perioada funcției variabile sinusoidale. Limitele integralei indică faptul că integrarea poate fi făcută în orice moment convenabil $$ t _ $$ și integrarea trebuie să fie delimitată exact o perioadă mai târziu. Pentru a înțelege mai bine toți termenii din ecuație. 1.9 și relațiile pe care le dețin, va trebui să examinăm puterea în circuite care sunt pur rezistive, pur inductive și pur capacitive.

Circuite pur rezistive

Dacă un circuit între terminale este pur rezistiv, curentul și tensiunea sunt în faza $$ (\ theta _ = \ theta _) $$. Astfel, ec. 1.9 poate fi redus la

$$ p = P + P \ cos (2 \ omega t) $$ (1.13)

Aceasta este denumită puterea reală instantanee. Figura 1.3 este un grafic al puterii reale instantanee pentru un circuit pur rezistiv, presupunând $$ \ omega = 377 \ mathrm< rad/s>$$. Puterea medie, P, este media lui p, pe o perioadă. Acest lucru poate fi văzut uitându-se la graficul în care P = 1 pentru circuit. Din figura 1.3, puterea reală instantanee nu poate fi niciodată negativă; cu alte cuvinte, puterea nu poate fi eliminată dintr-o rețea pur rezistivă. Deși puterea nu poate fi îndepărtată, este totuși disipată sub formă de energie termică.

Figura 1.3 Puterea reală instantanee și puterea medie a unui circuit pur rezistiv

Circuite pur inductive

Acum, dacă circuitul dintre terminale este pur inductiv, curentul și tensiunea sunt defazate cu $$ 90 ^. $$ Curentul circuitului întârzie tensiunea cu $$ 90 ^ $$ $$ (\ theta _= \ theta _-90 ^). $$ Ecuația puterii instantanee poate fi redusă la

$$ p = -Q \ sin (2 \ omega t) $$ (1,14)

În acest circuit pur inductiv, puterea medie este zero. Aceasta înseamnă că nu are loc nicio transformare a energiei din energie electrică în energie neelectrică. Puterea la terminale este schimbată continuu între circuit și sursa de alimentare care conduce circuitul la o frecvență de $$ 2 \ omega. $$ Ce înseamnă asta, atunci când p este pozitiv, energia este stocată în câmpurile magnetice asociate elementele inductive, iar atunci când p este negativ, energia este îndepărtată din câmpurile magnetice.

Puterea asociată cu circuitele pur inductive este cunoscută sub numele de putere reactivă Q. Puterea reactivă provine din caracterizarea unui inductor ca element reactiv. Pentru a face diferența între puterea medie și puterea reactivă, unitățile de wați (W) pentru puterea medie și var (volt-amp reactive, sau VAR) pentru puterea reactivă sunt utilizate. Figura 1.4 descrie puterea instantanee pentru un circuit pur inductiv, presupunând $$ \ omega = 377 \ mathrm< rads/s>$$ și Q = 1 VAR.

Figura 1.4 Puterea reală instantanee, puterea medie și puterea reactivă pentru un circuit pur inductiv

Circuite pur capacitive

În acest circuit pur capacitiv, curentul și tensiunea sunt $$ 90 ^ $$ defazate între ele. În acest caz, curentul conduce tensiunea cu exact 90 $ $ ^ $$ $$ (\ theta _= \ theta _ + 90 ^) $$. Expresia acestei puteri instantanee este dată de

$$ p = -Q \ sin (2 \ omega t) $$ (1,15)

În acest circuit, nu există nicio transformare a energiei din energie electrică în energie neelectrică, deoarece puterea medie este zero. Într-un circuit pur capacitiv, puterea este transferată continuu între sursa care furnizează energie și câmpul electric asociat elementelor capacitive. Figura 1.5 ilustrează puterea instantanee pentru un circuit pur capacitiv, presupunând $$ \ omega = 377 \ mathrm< rads/s>$$ și Q = -1 VAR.

Figura 1.5 Puterea reală instantanee și puterea medie pentru un circuit pur inductiv

Înțelegerea factorului de putere

Acest unghi $$ (\ theta _- \ theta _) $$ are un rol semnificativ în calculul puterii medii și a puterii reactive și este cunoscut sub numele de unghiul factorului de putere. Luând cosinusul acestui unghi se obține ceea ce este cunoscut sub numele de factor de putere, scurtat la pf și luarea sinusului acestui unghi este cunoscută sub numele de factor reactiv, scurtat la rf. Acest lucru poate fi notat ca:

$$ \ mathrm = \ cos (\ theta _- \ theta _) $$ (1,16)

$$ \ mathrm = \ sin (\ theta _- \ theta _) $$ (1,17)

Pentru a descrie complet unghiul factorului de putere, fie factor de putere întârziat sau factor de putere principal se folosesc termeni. Dacă factorul de putere rămâne în urmă, curentul rămâne în tensiune (adică este prezentă o sarcină inductivă). Pe de altă parte, dacă factorul de putere conduce, tensiunea conduce curentul (adică este prezentă o sarcină capacitivă).

Calculul conceptelor de putere CA.

O sarcină cuprinzând un rezistor 480 $$ \ Omega $$ în paralel cu un condensator $$ \ frac \ mu F $$ este conectată la bornele unei surse de tensiune variabilă sinusoidală $$ v _ $$, unde $$ v_ = 240 \ cos (5000t) \ mathrm< V>$$

A) Care este valoarea de vârf a puterii instantanee furnizate de sursa de alimentare?

Calculul reactanței capacitive:

Calculul puterii reactive câștigate de sursă:

Calculul valorii maxime a puterii instantanee livrate:

B) Care este valoarea de vârf a puterii instantanee absorbite de sursă?

C) Care este puterea medie livrată sarcinii?

Folosind ecuația de putere din partea A, $$ = \ frac> $$

Puterea medie este $$ P = 60 \ mathrm< V>$$

D) Care este puterea reactivă livrată sarcinii?

Folosind ecuația puterii reactive din partea A, $$ = \ frac> $$

E) Este sarcina care absoarbe sau generează varele magnetizante?

Folosind ecuația puterii reactive din partea A, $$ = \ frac> $$

$$ Q = -80 \ mathrm< VAR>$$ O valoare negativă înseamnă că sarcina generează varuri magnetizante.

F) Care este factorul de putere?

Folosind ecuația factorului de putere, $$ = \ frac + \ frac> $$

Prin urmare, factorul de putere este $$ pf = 0,6 $$ lider

G) Care este factorul reactiv?

Folosind ecuația factorului reactiv, $$ \ sin (0 ^ -53.267 ^) $$

Prin urmare, factorul reactiv este $$ rf = -0.8 $$