Introducere: modelul ideal de gaz, căldură, lucru și termodinamică

Imaginea teoriei cinetice a unui gaz (prezentată în prelegerea anterioară) este deseori numită Modelul ideal de gaz.În ignoră interacțiunile dintre molecule și dimensiunea finită a moleculelor. De fapt, acestea devin importante doar atunci când gazul este foarte aproape de temperatura la care devine lichid sau sub presiune extrem de mare. În această prelegere, vom analiza comportamentul gazelor în intervalul de presiune și temperatură corespunzător motorul termic, iar în această gamă Modelul ideal de gaz este o aproximare excelentă. În esență, programul nostru de aici este de a învăța cum gazele absorb căldura și o transformă în lucru și invers. În această interacțiune căldură-muncă se numește termodinamică.

Julius Robert Mayer a fost primul care a apreciat că există o echivalență între căldură și lucru mecanic. Calea sinuoasă care l-a condus la această concluzie este descrisă într-o prelegere anterioară, dar odată ce a fost acolo, și-a dat seama că, de fapt, echivalența numerică - câți Jouli dintr-o singură calorie în terminologia actuală - ar putea fi calculată cu ușurință din rezultate. a unor măsurători ale căldurii specifice gazelor de către oamenii de știință francezi. Cheia a fost că au măsurat călduri specifice atât la volum constant și la presiune constantă.Mayer și-a dat seama că, în acest din urmă caz, încălzirea gazului a crescut în mod necesar volumul său și, prin urmare, gazul a funcționat prin împingerea extinderii containerului său. După ce sa convins că munca mecanică și căldura sunt echivalente, evident că căldura suplimentară necesară pentru creșterea temperatura gazului la presiune constantă a fost exact lucrarea pe care gazul a făcut-o pe containerul său. (Notă istorică: deși a făcut treaba în 1842, nu a publicat până în 1845 și, la început, a calculat greșit - dar apoi a dat o cifră de 1% din valoarea corectă de 4,2 jouli pe calorie.)

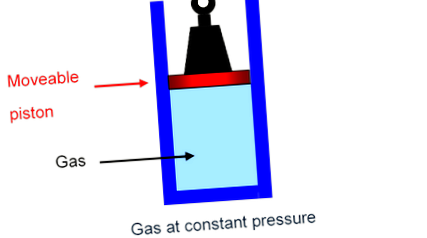
Cel mai simplu mod de a vedea ce se întâmplă este să vă imaginați gazul dintr-un cilindru, ținut de un piston, cu o greutate fixă, capabil să se miște în sus și în jos cilindrul fără probleme cu frecare neglijabilă. В Presiunea pe gaz este doar greutatea totală presată în jos împărțită la aria pistonului, iar această greutate totală, desigur, nu se va schimba pe măsură ce pistonul se mișcă încet în sus sau în jos: gazul este la presiune constantă.

ideal

CV-ul pentru încălzirea specifică gazului și CP

Luați în considerare acum cele două călduri specifice ale aceluiași eșantion de gaz, să zicem un mol:

Căldură specifică la volum constant, C V В (piston lipit pe loc),

Căldură specifică la presiune constantă, C P В (piston liber să crească, fără frecare).

De fapt, am elaborat deja CV lecture în cursul teoriei cinetice: la temperatura T, В reamintim că energia cinetică medie pe moleculă este de 3 2 k BT, astfel încât un mol de gaz - numărul de molecule al lui Avogadro - va avea energie cinetică totală, pe care o vom eticheta energie internă,

E int = 3 2 k B T ⋅ N A = 3 2 R T .

(În acest caz cel mai simplu, ignorăm posibilitatea ca moleculele să aibă propriile lor energie internă: s-ar putea să se rotească sau să vibreze - vom include asta în scurt timp)

Că energia internă este de 3 2 R T ² pe mol ne dă imediat căldura specifică a unui mol de gaz într-un volum fix,

aceasta fiind căldura care trebuie furnizată pentru a crește temperatura cu un grad.

Cu toate acestea, dacă gazul, în loc să fie într-o cutie fixă, este ținut într-un cilindru la presiune constantă, experimentul confirmă că mai mult trebuie furnizată căldură pentru a crește temperatura gazului cu un grad.

După cum și-a dat seama Mayer, energia termică totală care trebuie furnizată pentru a crește temperatura gazului cu un grad la presiune constantă este 3 2 k B In pe moleculă plus energia necesară pentru ridicarea greutății.

Munca pe care gazul trebuie să o facă pentru a crește greutatea este forța pe care gazul o exercită asupra pistonului înmulțită cu distanța de deplasare a pistonului.

Dacă aria pistonului este A, B, atunci gazul la presiunea P B exercită forța P A. În În

Dacă la încălzirea cu un grad, pistonul crește la o distanță de Δ h, gazul funcționează

P A ⋅ Δ h = P Δ V .

Acum, pentru un mol de gaz, P V = R T, В deci la P constant constantă

Prin urmare, munca făcută de gaz în creșterea greutății este doar R Δ T, В căldura specifică la presiune constantă, energia termică totală necesară pentru a crește temperatura unui mol cu ​​un grad,

De fapt, această relație este adevărată indiferent dacă moleculele au sau nu energie internă de rotație sau vibrațională (este cunoscută sub numele de relația lui Mayer.) În De exemplu, căldura specifică a oxigenului la volum constant

C V (O 2) = 5 2 R

și aceasta este înțeleasă ca o contribuție de 3 2 R B din energia cinetică și R B din cele două moduri de rotație ale unei molecule cu gantere (doar de ce nu există o rotație a formei de contribuție în jurul celei de-a treia axe poate fi înțeleasă doar folosind mecanica cuantică). căldura specifică a oxigenului la presiune constantă

C P (O 2) = 7 2 R .

Merită să aveți un simbol standard pentru raport dintre căldurile specifice:

Urmărirea unui gaz în (P, V) Avion: izoterme și adiabate

Un gaz ideal într-o cutie are trei variabile termodinamice: P, V, T. В В Dar dacă există o masă fixă ​​de gaz, fixarea a două dintre aceste variabile o fixează pe a treia din P V = n R T В (pentru n В moli). Într-un motor cu căldură, căldura poate pătrunde în gaz, apoi poate ieși într-o etapă diferită. Gazul se poate extinde lucrând sau se poate contracta pe măsură ce se lucrează la acesta., trebuie să urmărim starea variabilă a gazului. Faceți acest lucru urmărind o curbă în planul (P, V) В.

Furnizarea de căldură unui gaz care în consecință se extinde și efectuează lucrări mecanice este cheia motorului termic. Dar doar știința faptului că un gaz se extinde și lucrează nu este suficientă informație pentru a-și urma calea în planul (P, V). traseul pe care îl urmează va depinde de faptul dacă este furnizată sau nu căldură în același timp. Există, totuși, două moduri particulare în care un gaz se poate extinde reversibil - ceea ce înseamnă că o modificare mică a condițiilor externe ar fi suficientă pentru ca gazul să-și reia drumul în planul (P, V) В înapoi. Este important să ne concentrăm pe căi reversibile, deoarece așa cum a demonstrat Carnot și vom discuta mai târziu, acestea corespund celor mai eficiente motoare. seturile de căi reversibile sunt izotermele și adiabatele.

Comportament izotermic:В В gazul este menținut la temperatură constantă prin permiterea fluxului de căldură înainte și înapoi cu un obiect foarte mare (un „rezervor de căldură”) la temperatura T. В В De la PV = n RT, В este evident că pentru o masă fixă ​​de gaz, menținută la constantă T В, dar supusă unei presiuni (încet) variabile, variabilele P, V В vor urmări o cale hiperbolică în (P, V) В avion.В

Această cale, P V = n R T 1, B spune că se numește izotermă la temperatura T 1. В В В Iată două exemple de izoterme:

Comportament adiabatic: „Adiabatic” înseamnă „nu trece nimic”, în acest caz nu intră sau iese căldură a gazului prin pereți. Deci toată munca făcută la comprimarea gazului trebuie să intre în energia internă E int .

Pe măsură ce gazul este comprimat, acesta urmează o curbă în planul (P, V) В numită adiabat.În Pentru a vedea cum diferă un adiabat de o izotermă, imaginați-vă începând la un moment dat pe izoterma albastră 273K din graficul de mai sus și aplicând presiune astfel încât gazul să se deplaseze la presiune mai mare și volum mai mic. Deoarece energia internă a gazului este în creștere, dar numărul de molecule rămâne același, temperatura acestuia este în mod necesar în creștere, se va deplasa spre curba roșie, apoi deasupra ei. În acest sens, adiabatele sunt întotdeauna mai abrupte decât izotermele..ÎN

În diagrama de mai jos, am adăugat câteva adiabate la izoterme:

Ecuație pentru un Adiabat

Ce ecuație pentru un adiabat corespunde P V = n R T 1 В pentru o izotermă? В

La creșterea temperaturii gazului cu Δ T, В schimbarea energiei interne - suma energiei cinetice moleculare, a energiei de rotație și a energiei vibraționale (dacă există),

Δ E int = C V Δ T .

Acest lucru este întotdeauna adevărat: indiferent dacă gazul schimbă volumul sau nu este irelevant, tot ceea ce contează în E int В este suma energiilor moleculelor individuale (presupunând, așa cum facem noi, că forțele de atracție sau de respingere dintre molecule sunt neglijabile).

În compresia adiabatică, toată munca făcută de presiunea externă merge în această energie internă, deci

(Desigur, comprimarea gazului dă negativ Δ V, В pozitiv Δ E int. В)

Pentru a găsi ecuația unui adiabat, luăm limita infinitesimală

împărțiți partea stângă cu P V, В partea dreaptă cu n R T В (deoarece P V = n R T,

În asta e OK) a găsi

- R C V d V V = d T n T .

- R C V d V V = d T n T .

Reamintim acum că C P = C V + n R, B și C P/C V = γ. În Rezultă că

n R C V = C P - C V C V = γ - 1.

- (γ - 1) ∫ d V V = ∫ d T T

ln T + (γ - 1) ln V = const .

din care este ecuația unui adiabat

T V γ - 1 = const .

Din P V = n R T, ecuația P, V В pentru un adiabat poate fi găsită înmulțind partea stângă a acestei ecuații cu constanta P V/T, В В dând

P V γ = const. Pentru un adiabat,

unde γ = 5 3 В pentru un gaz monatomic, 7 5 В pentru un gaz diatomic.