Dr. Farrokh Alemi.
Dr. Duncan Neuhauser.
Acest capitol vă ajută să construiți o diagramă de control pentru dieta și tiparele de exerciții. În acest moment al efortului dvs. de îmbunătățire, este posibil să fi făcut o schimbare în stilul dvs. de viață, să fi colectat date despre greutate sau modele de exerciții și vă întrebați dacă schimbarea a dus la îmbunătățire. Întrebarea cheie este dacă greutatea actuală și timpul de exercițiu se compară favorabil cu modelele istorice.
Dacă sunteți ca majoritatea oamenilor, greutatea și timpul de exerciții fluctuează foarte mult. Există multe motive pentru această variație. Uneori, greutatea sau tiparele de exercițiu nu sunt măsurate cu precizie. Uneori se introduc variații pentru că uitați să luați o măsură. Uneori, greutatea ta fluctuează cu câteva kilograme doar pe baza absorbției de apă sau a hainelor pe care le porți. Toate aceste fluctuații fac dificilă evaluarea dacă valorile noi sunt diferite de valorile istorice. Pierderea în greutate de cinci kilograme despre care ați putea fi extaziat ar putea fi doar o variație aleatorie. Un anumit nivel de creștere și cădere este natural; adevărata întrebare este dacă noua dvs. greutate și modelele de exerciții indică o adevărată abatere de la nivelurile istorice. O diagramă de control vă poate ajuta să răspundeți la această întrebare.
Acest capitol presupune că puteți trasa date, puteți comanda numere de la mici la mari și puteți calcula rădăcina pătrată a unui număr. Acestea sunt sarcini relativ simple, dar este posibil ca unele persoane să aibă puțină experiență în manipularea datelor. Acest tip de analiză are nevoie de timp și răbdare. Dacă nu vă simțiți confortabil când analizați datele, vă recomandăm să căutați pagini web în care furnizați datele dvs., iar webul va desena diagrama de control pentru dvs. (consultați http://www.rapidimprovements.com). Desigur, puteți, de asemenea, să cereți unui prieten sau unui clinician să vă facă analiza.
Cu o diagramă de control, vă monitorizați progresul în timp. Creați un grafic, în care axa x este de zile (ziua zero fiind momentul în care ați început programul) și axa y este rezultatul pe care îl monitorizați. Pentru a decide dacă rezultatele dvs. sunt diferite de modelele istorice, se calculează limitele de control superioare și inferioare (UCL și respectiv LCL). Aceste limite sunt organizate pentru a constitui un astfel de interval încât, dacă modelul dvs. istoric a continuat, datele de 99% din timp limitele de control superioare și inferioare sunt calculate utilizând formule matematice specifice tipului de rezultat pe care îl monitorizați. Acest capitol vă arată cum să calculați aceste limite în funcție de dacă vă monitorizați greutatea, timpul de exercițiu, zilele de dietă pierdute, zilele de exerciții pierdute sau alte rezultate similare.
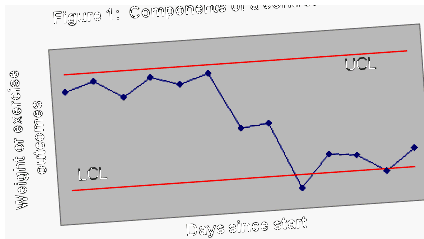
Figura 1 prezintă structura unei diagrame tipice de control. În această figură, toate punctele, cu excepția a două, se încadrează în limitele de control.
Cum să citiți o diagramă de control?
O diagramă de control este utilă în multe moduri. Punctele în afara limitelor sunt neobișnuite și marchează abaterea de la tiparele istorice. Ați slăbit dacă noua dvs. măsură este sub limita inferioară de control. Două puncte din figura 1 scad sub LCL - și, prin urmare, semnalează o pierdere în greutate. Celelalte puncte nu indică nicio pierdere reală în greutate, chiar dacă există un număr dintre ele care arată o scădere în greutate. Aceste mici fluctuații sunt aleatorii și nu diferă de modificările istorice ale greutății dvs.
Puteți utiliza o diagramă de control pentru a vedea dacă timpul de exercițiu depășește limita superioară de control. Dacă da, ești liniștit că exersezi mai mult. Dacă Figura 1 a măsurat durata exercițiului, am concluziona că nu a existat nicio creștere a timpului de exercițiu, deoarece niciunul dintre puncte nu depășește limita superioară de control.
De asemenea, puteți utiliza graficul de control pentru a vedea dacă vă mențineți câștigurile din perioadele de timp anterioare. Dacă datele dvs. se încadrează în limitele de control, în ciuda variațiilor de zi cu zi, nu a existat nicio modificare a greutății și a timpului de exercițiu. Dacă sunteți la greutatea și exercițiul ideal, atunci doriți ca datele dvs. să se încadreze în limite.
Numărul minim de observații
Cu cât aveți mai multe date, cu atât aveți mai multă precizie în construirea limitelor de control superioare și inferioare. Cel puțin, aveți nevoie de cel puțin șapte puncte de date în perioada de pre-intervenție pentru a începe majoritatea graficelor. Nu toate datele sunt utilizate pentru calcularea limitelor de control; de multe ori limitele se bazează pe perioada de pre-intervenție. Observațiile ulterioare post-intervenție sunt apoi comparate cu limitele de pre-intervenție. Dacă vreun punct nu se încadrează în limite, puteți concluziona că intervenția v-a schimbat greutatea sau tiparele de exerciții. Vezi Figura 2 pentru un exemplu de stabilire a limitelor pe baza perioadelor de pre-intervenție.
Figura 2: Date post intervenție comparativ cu
limite pe baza perioadei de pre-intervenție
Zile de la început
Comparați graficul din Figura 2 cu graficul din Figura 1. Ambele se bazează pe aceleași date, dar Figura 2 stabilește limitele de control superioare și inferioare pe baza primelor șapte zile, înainte de intervenție. Figura 2 arată că datele post-intervenție sunt mai mici decât LCL și, prin urmare, s-a produs o schimbare semnificativă. Când Figura 2 este comparată cu Figura 1, vedem că mai multe puncte sunt în afara limitelor din Figura 2. Prin stabilirea limitelor tiparelor de pre-intervenție, am putut detecta mai precis îmbunătățirile de la intervenție.
Formulele matematice pentru calcularea limitelor de control depind de ceea ce încercați să monitorizați. Mai jos enumerăm calculul limitelor de control pentru două tipuri de măsuri:
- Limite pentru valorile numerice. Aceste limite sunt folosite pentru a analiza numerele continue (de exemplu, monitorizarea greutății pe zi, numărul de calorii pe zi, minutele de exerciții pe zi, numărul de căni de cafea pe zi, numărul de produse alimentare nesolicitate pe zi sau numărul de țigări fumate pe zi).
- Limite pentru zilele ratate. Aceste limite sunt stabilite pentru observații discrete, care se exclud reciproc (de exemplu, zile de dietă pierdute, zile de antrenament pierdut, zile fără cafea, zile fără junk food sau zile fără fum).
Acum vom discuta separat despre fiecare dintre aceste limite.
Limite pentru valorile numerice (abordarea lui Tukey)
Vom folosi limitele sugerate de Tukey pentru calcularea intervalelor de încredere pentru medianele valorilor numerice, cum ar fi greutatea sau durata exercițiului. [1] Procedura calculează limitele de control din „A patra răspândire” - diferența dintre a patra, (unde j din punctele de date sunt sub această valoare) și Trei-Patrimi (unde ѕ din punctele de date sunt sub această valoare). Majoritatea cititorilor sunt familiarizați cu mediana, o valoare peste care se află jumătate din date și sub care, din nou, jumătate din date sunt. Un al patrulea este mediana jumătății inferioare a datelor, iar Trei pătrimi este mediana jumătății superioare a datelor. UCL este suma celor trei pătrimi și de 1,5 ori a patra răspândire. Limita inferioară de control este a patra minus de 1,5 ori a patra marjă.
Procedură pentru calcularea limitelor de control ale lui Tukey
- Enumerați valorile de observație în ordine crescătoare.
- Calculați mediana, care are 50% din datele de sub ea și 50% mai sus.
- Dacă numărul de observații este impar, mediana este observația de mijloc. De exemplu, dintre cele cinci numere 1, 3, 4, 5 și 7, mediana este 4.
- Dacă numărul observațiilor este egal, luați media celor două numere de rang mediu. De exemplu, dintre cele patru numere 1, 3, 4 și 5, mediana este 3,5.
- Un al patrulea este mediana celor mai mici 50% din date, date de la cea mai mică valoare și, uneori, inclusiv mediana.
- Dacă mediana întregului set de date este un punct de date real, includeți-l în cel mai mic 50% din date.
- A Trei pătrimi este mediana primelor 50% din date, date din (și uneori incluzând) mediana întregului set de date la cea mai mare valoare.
- Dacă mediana întregului set de date este un punct de date real, includeți-l în cel mai mare 50% din setul de date.
- Calculați a patra răspândire ca diferență între valorile a patra și a trei-a patra.
- Calculați UCL și LCL folosind următoarele două formule:
LCL = A patra - 1,5 * A patra răspândire
Să vedem un exemplu în care aceste calcule sunt puse în funcțiune. Jane a colectat date în Tabelul 1 cu privire la timpul de exercițiu. Plănuia să facă mișcare de 3 ori pe săptămână și de fiecare dată când făcea mișcare, înregistra timpul în minute. Când nu a exercitat, a înregistrat un zero pentru durata exercițiului. Primele șapte zile înregistrate au fost pre-intervenție. După această perioadă, ea și soțul ei s-au alăturat unei echipe mixte de volei. Voia să știe dacă aderarea la echipă a făcut o diferență în timpul ei de antrenament.
- Energetica controlului obezității și a greutății Contează compoziția dietei Știința directă
- Diabetul controlează mai bine cu dieta slab glicemică Reuters
- Controlul prejudecății în studiile dietetice pentru prevenirea recidivelor coronariene Studiul european al dietei Lyon
- Dieta fără gluten ajută la controlul convulsiilor în epilepsie
- Exemple de alimente, listă de produse alimentare și rețete pentru dieta de control al vitezei de croazieră vă protejează sănătatea