Abstract
În această lucrare, analizând structura subțire Lefschetz-degetar, investigăm fazele cuantice (sau punctele critice cuantice) în teoriile câmpului scalar zero-dimensional cu acțiuni complexe. Folosind primele principii, derivăm ecuațiile degetare ale acestor modele pentru diferite valori ale parametrilor de cuplare. În descompunerea degetului de integrale de cale complexe, determinarea așa-numitelor numere de intersecție apare ca un ingredient important. În această lucrare, obținem expresiile analitice pentru numărul de intersecție combinat de degetare și anti-degetare ale acestor teorii zero-dimensionale. De asemenea, derivăm expresiile condiționale care implică relații între parametrii de cuplare ai modelului, care ne-ar ajuta să prezicem tranzițiile de fază cuantice în aceste sisteme. Vedem că structura degetară subiacentă suferă o schimbare drastică atunci când sistemul trece printr-o astfel de tranziție de fază.
Introducere
Intalnim integrale de cale cu actiuni complexe in multe ramuri ale fizicii. Exemplele proeminente sunt integralul căii Minkowski, teoria Yang-Mills în vidul theta, teoriile gabaritului Chern-Simons, teoriile gabaritului chiral și QCD cu potențial chimic. Există, de asemenea, teorii cuantice cu acțiuni complexe, care sunt invariante sub \ (> \) simetrie [1,2,3]. În contextul teoriei șirurilor, modelul matricei IKKT, o teoria câmpului cuantic supersimetric zero-dimensional, care servește ca un candidat promițător pentru o formulare neperturbativă a teoriei superstringului, are un operator fermionic complex [4,5,6]. Investigarea structurii neperturbative a unor astfel de teorii folosind metode tradiționale integrale de cale Monte Carlo nu este fiabilă din cauza prezenței problemei semnelor. Ar fi foarte util să existe un formalism care să ofere un instrument promițător pentru rezolvarea teoriilor câmpului cuantic care conțin astfel de greutăți integrale ale căilor complexe.
O metodă recentă și în curs de dezvoltare pentru a trata teoriile câmpului cuantic cu acțiuni complexe utilizează analogul complex al teoriei Morse din topologia diferențială [7, 8]. Nota de subsol 1 Acolo, obiectele de interes primar, așa-numitele degetare Lefschetz, sunt un set de sub-varietăți asociate cu o funcție care satisfac ecuația fluxului Morse pentru partea reală a funcției. Ideea centrală din spatele utilizării acestui formalism este de a reformula calea integrală în termenii unui set finit de integrale non-oscilatorii. Lucrări recente despre integrale de cale complexă și conexiuni la degetare Lefschetz, inclusiv aplicații la tuneluri cuantice și amplitudini de împrăștiere pot fi văzute în Refs. [18,19,20,21,22,23,24,25,26,27,28,29]. În Ref. [30,31,32,33,34,35] abordarea Lefschetz-degetar a fost utilizată pentru a studia teoriile câmpului cuantic bosonic și în Refs. Au fost studiate [36,37,38,39,40,41,42,43] modele care includ fermioni. Relevanța degetelor Lefschetz în contextul expansiunii semi-clasice în teoriile câmpului cuantic cu valoare asimptotică este discutată în Ref. [44,45,46,47,48].
Lucrarea este organizată după cum urmează. În sectă. 2 oferim un primer asupra degetelor Lefschetz prin introducerea ecuațiilor de flux de gradient ale acțiunii date. În sectă. 3 introducem modelul interesului nostru, un model bosonic zero-dimensional cu acțiune complexă care conține interacțiuni quartice și un termen sursă. Ecuațiile degetar pentru acest model sunt derivate în continuare în Sect. 4. Discutăm expresii analitice pentru ecuațiile degetar și anti-degetar și așa-numitele soluții fantomă, care nu sunt nici degetare, nici anti-degetare. De asemenea, discutăm comportamentul funcției de partiție și observabilele modelului în funcție de parametrii de control. În sectă. 5 discutăm limitele tranzițiilor de fază pentru diverse combinații ale valorilor parametrilor de cuplare. Acesta include cazul interesant atunci când acțiunea complexă prezintă simetrie \ (> \). Câteva exemple de limite de tranziție de fază sunt furnizate în secțiunea. 6. Exemplele arată că structura degetelor suferă o schimbare drastică atunci când parametrii de guvernare (non-termici) ai modelului trec printr-un punct critic cuantic. În sectă. 7 oferim un rezumat al principalelor rezultate, iar în sect. 8 oferim concluziile noastre și indicăm posibile direcții viitoare.
Un exemplu este degetarii Lefschetz
Intuitiv, putem raporta degetele Lefschetz la ciclul de integrare original al teoriei câmpului cuantic în felul următor. Să denotăm ciclul de integrare inițial ca \ (> _ >> \). „Complexificăm” acest colector în \ (> _ >> \), adică luăm un colector complex \ (> _ >> \) care conține colectorul original \ (> _ >> \) ca submanifold, cu cerința ca conjugatul complex al unui element al lui \ (> _ >> \) să fie elementul în sine. Se poate gândi la \ (> _ >> => ^ \) și la \ (> _ >> => ^ \) pentru ușurința înțelegerii.
După complexificare, identificăm Funcția Morse [51]. Funcția Morse într-un sens liber determină aceste degetare. O funcție naturală de luat în considerare este acțiunea. (Funcția Morse reală luată în considerare este partea reală a \ (- S \) deoarece, prin definiție, funcțiile Morse sunt reale.) Având în vedere o funcție Morse, identificăm puncte critice - puncte în \ (> _ >> \) unde funcția Morse este extremizată local. Următorul pas, vizual, poate fi gândit ca deformându-se continuu \ (> _ >> \), deformarea fiind controlată de funcția Morse prin ecuațiile fluxului Morse
unde \ (g ^> \) este metrica de pe \ (> _ >> \) și \ (z_\) sunt un set de coordonate locale în jurul punctelor critice ale S. Se poate verifica imediat dacă partea imaginară a acțiunii S este constant de-a lungul soluției la ecuațiile de mai sus.
Ca rezultat final al acestei construcții, obținem o pereche de sub-colectoare, numite degetar și anti-degetar, asociate cu fiecare punct critic. Degetarul este soluția „stabilă”. Adică, acțiunea merge la infinit suficient de repede de-a lungul unui degetar, astfel încât să păstreze integrala care implică \ (\ exp (-S) \) pentru a fi convergentă. Anti-degetarul este soluția „instabilă”. Un exemplu familiar în fizică este metoda celei mai abrupte coborâri și, prin urmare, formalismul degetelor Lefschetz poate fi considerat ca generalizarea celei mai abrupte metode de coborâre. Un tratament riguros al acestei construcții poate fi găsit în Ref. [51,52,53].
O integrală care implică acțiunea pe sub-colectorul \ (> _ >> \) poate fi acum scrisă ca o combinație liniară de integrale peste degetarii Lefschetz. În acest limbaj, expresia pentru funcția de partiție asociată unui sistem cu acțiune S este dată ca suma ponderată a contribuțiilor din punctele critice ale acțiunii
unde integrala denotă integrarea peste degetul Lefschetz \ (> _ i \), care este asociat cu eu-punctul critic \ (\ phi _i \) al acțiunii. Greutatea (cunoscută și sub numele de intersecție) \ (n_i \) este un număr întreg care decide contribuția unui anumit punct critic la funcția de partiție. Presupunând că punctele critice nu împărtășesc un flux de gradient comun, dat în ecuație. (2.1), \ (n_i \) este dat de numărul de ori în care anti-degetul intersectează ciclul de integrare original \ (> \) [54]. Acesta este,
Un avantaj al utilizării degetelor Lefschetz este că pe aceste degetare, așa cum am discutat mai sus, partea imaginară a acțiunii rămâne constantă. Aceasta este cu siguranță o proprietate de dorit, deoarece, în calea (euclidiană) formalismul integral al teoriilor câmpului cuantic, partea imaginară constantă a acțiunii, \ (\ mathrm (S) \), în integral, Eq. (2.2), poate fi extras ca factor de fază, iar integrala rămasă devine o integrală neoscilatorie. Nota de subsol 2
În dimensiunile spațiu-zero, formalismul se simplifică foarte mult. Pentru majoritatea situațiilor luate în considerare în această lucrare, ciclul original de integrare este linia reală, \ (> \). În acest caz, ajungem să avem de-a face cu curbe în planul gradelor de libertate permise pentru câmpurile (adică \ (> \)) care satisfac ecuația fluxului de gradient
Unde t este un parametru, iar linia superioară reprezintă conjugarea complexă. Degetarul \ (_ i \) asociat cu punctul critic \ (\ phi _i \) al acțiunii este definit ca soluția la ecuație. (2.4) care satisface
iar anti-degetarul \ (_ i \) satisface
Prin definiție, degetele se termină întotdeauna în interiorul regiunilor de stabilitate, Nota de subsol 3, în timp ce anti-degetele se termină în interiorul regiunilor de instabilitate.
Model quartic cu un termen sursă
Să luăm în considerare o teorie cuantică a câmpului în dimensiuni zero-spațiu-timp, cu acțiunea dată în următoarea formă
Acțiunea are un termen de interacțiune quartic și un termen sursă - este cea mai simplă acțiune cuantică nontrivială a teoriei câmpului cu un termen sursă. Parametrii \ (\ sigma \), \ (\ lambda \) și h sunt în general complexe. Pentru comoditate, exprimăm și noi
Motivația pentru luarea în considerare a acestei acțiuni este dublă. În primul rând, acțiunea de mai sus acționează ca un model de jucărie excelent pentru înțelegerea sistemelor cu acțiuni complexe, în calea formalismului integral [34, 49, 55, 56] și modul în care degetele Lefschetz contribuie la atenuarea problema semnelor, în același timp nefiind prea banal și ne permite să prezentăm o mulțime de dinamici bogate care însoțesc analiza degetului Lefschetz. Acțiunea de mai sus, cu complex \ (\ sigma \) este relevantă pentru gazul Bose relativist cu potențial chimic diferit de zero [57, 58]. O variantă a acestui model, cu complexele \ (\ sigma = h = 0 \) și \ (\ lambda \) a fost studiată în Ref. [55]. În al doilea rând, pentru metoda utilizată în calculele noastre, interacțiunile quartice sunt termenii cei mai înalți, exact rezolvabili datorită teoremei Abel - Ruffini din algebră [59] care afirmă că nu există expresii în formă închisă pentru soluții la ecuațiile polinomiale generale de gradul cinci sau mai sus. În plus, includerea unui termen sursă ne asigură că vom epuiza toate situațiile posibile din punct de vedere fizic pentru un sistem cu interacțiuni quartice.
Să începem cu determinarea regiunilor de stabilitate (denumite uneori și Stokes pene [46, 77]) în acest model. Întrucât integralul din ecuație. (2.2) implică expresia \ (\ text (-S) \), integralul este convergent în regiuni în care, pe măsură ce \ (\ phi \) se apropie de infinit, \ (\ text (S [\ phi]) \ ge 0 \ ). Deoarece ordinea cea mai înaltă din acțiunea noastră este de patru, obținem patru pene în planul complex în care integralul este convergent. Acest lucru este prezentat schematic în Fig. 1.
O reprezentare schematică a regiunilor de stabilitate la infinit pentru acțiunea dată în ecuație. (3.1). În interiorul regiunilor umbrite, integrala din ecuație. (2.2) este convergent. În general, poziția și forma acestor pene sunt controlate de parametrii \ (\ sigma, \ lambda \) și h în acțiune
O modalitate de a găsi (anti-) degetarul asociat cu un punct critic este rezolvarea ecuației fluxului de gradient, ecuația. (2.4), pentru (anti) degetare. Această metodă devine însă foarte complicată, chiar și pentru forme simple de acțiuni, datorită cuplării dintre părțile reale și imaginare ale ecuației diferențiale. Din fericire, există o altă metodă mai simplă. Putem exploata o proprietate foarte crucială a (anti) degetelor: partea imaginară a acțiunii rămâne constantă de-a lungul acestor (anti) degetare. Prin urmare, pentru a rezolva degetele, căutăm soluții la constrângere
cu \ (\ phi _i \) care indică punctul critic.
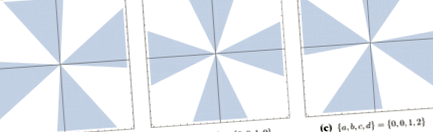
Soluțiile la ecuația degetului date în ecuație. (3.3), corespunzător punctelor critice \ (\ phi _0 \) și \ (\ phi _ \ pm \), pentru parametrii \ (\< a = 1, b = 1, c = 1, d = 0, h = 0 \>\). În toate cele trei figuri, curbele solide verzi reprezintă degetarele, curbele punctate roșii reprezintă anti-degetele, iar curbele solide gri reprezintă fantomele. Regiunile umbrite reprezintă regiunile în care \ (\ text (S) \ ge 0 \)
Să ne restrângem calculele la cazurile în care h (parametrul care controlează termenul liniar în acțiune) este mic în comparație cu \ (\ sigma \) și \ (\ lambda \). Restricționăm în continuare h să fie fie real, fie pur imaginar. Acest lucru ne permite să aproximăm cele trei puncte critice Nota de subsol 4 a acțiunii ca
Punctul critic \ (\ phi _0 \) este aproape de origine (adică \ (\ phi = 0 \)) pentru mici h în timp ce poziția \ (\ phi _ \ pm \) depinde de alegerea parametrilor. Să denotăm partea imaginară a acțiunii la un punct critic dat de \ (\ rho _i \). Acesta este,
Pentru acțiunea specială pe care o luăm în considerare, acestea iau următoarele forme
- Masking Bitter Taste by Molecules SpringerLink
- Îmbunătățirea eficienței ecranelor cu un motor electromagnetic liniar SpringerLink
- Loxapina pentru inversarea tulburărilor metabolice induse de antipsihotice O diagramă de revizuire SpringerLink
- Cum se schimbă tatuajele când slăbești - Idei de tatuaje, artiști și modele
- Energetica de incubație a Laysan Albatros SpringerLink