Sabyasachi Das
Departamentul de anestezie și îngrijire critică, Colegiul de Medicină, Kolkata, Bengalul de Vest, India
Koel Mitra
Departamentul de anestezie și îngrijire critică, Colegiul de Medicină, Kolkata, Bengalul de Vest, India
Mohanchandra Mandal
1 Departamentul de anestezie și îngrijire critică, North Bengal Medical College, Sushrutanagar, Darjeeling, West Bengal, India
Abstract
Abordarea unei dimensiuni a eșantionului este o problemă practică care trebuie rezolvată în timpul etapei de planificare și proiectare a studiului. Scopul oricărei cercetări clinice este de a detecta diferența reală între două grupuri (putere) și de a furniza o estimare a diferenței cu o precizie rezonabilă (precizie). Prin urmare, cercetătorii ar trebui să facă o estimare a priori a dimensiunii eșantionului cu mult înainte, înainte de a efectua studiul. Calculul dimensiunii eșantionului post hoc nu este încurajat în mod convențional. Dimensiunea adecvată a eșantionului minimizează eroarea aleatorie sau, cu alte cuvinte, reduce ceva care se întâmplă întâmplător. Un eșantion prea mic poate să nu răspundă la întrebarea de cercetare și poate avea o validitate îndoielnică sau poate oferi un răspuns imprecis, în timp ce un eșantion prea mare poate răspunde la întrebare, dar este intensiv în resurse și, de asemenea, poate fi lipsit de etică. Este necesară o mai mare transparență în calcularea dimensiunii eșantionului, astfel încât să poată fi justificată și reprodusă în timpul raportării.
INTRODUCERE
Până la sfârșitul acestui articol, cititorul va putea enumera condiția prealabilă pentru estimarea mărimii eșantionului, pentru a descrie cadențele comune ale calculului mărimii eșantionului și importanța estimării a priori a mărimii eșantionului. Cititorii vor putea defini terminologiile comune legate de calculul dimensiunii eșantionului.
IMPORTANȚA STUDIULUI PILOT ÎN ESTIMAREA MĂRIMII EȘANTIONULUI
În literatura publicată, datele relevante pentru calcularea dimensiunii eșantionului pot fi obținute din estimări de prevalență sau rate de evenimente, deviație standard (SD) a rezultatului continuu, dimensiunea eșantionului de studii similare cu rezultate similare. Ideea estimărilor aproximative ale „efectului” poate fi obținută prin revizuirea metaanalizei și a efectului semnificativ clinic. Studiu pilot mic, experiență personală, opinia experților, presupuneri educate, registre de spitale, rapoarte nepublicate susțin cercetătorul atunci când avem informații insuficiente în literatura de specialitate existentă/disponibilă. Un studiu pilot nu numai că ajută la estimarea dimensiunii eșantionului, ci și scopul său principal este de a verifica fezabilitatea studiului.
Studiul pilot este un test pe scară mică, desfășurat ca pre-test și se încearcă pentru studiul major propus. Permite testarea preliminară a ipotezelor și poate sugera unele modificări, renunțarea la o parte sau dezvoltarea unor noi ipoteze, astfel încât să poată fi testată mai precis. [8] Poate aborda multe probleme logistice, cum ar fi verificarea faptului că instrucțiunile sunt cuprinzătoare, iar anchetatorii sunt calificați în mod adecvat pentru proces. Studiul pilot oferă aproape întotdeauna suficiente date pentru ca cercetătorul să decidă dacă va continua studiul principal sau să îl abandoneze. Multe idei de cercetare care par să arate o mare promisiune sunt neproductive atunci când sunt efectiv realizate. Din concluziile studiului pilot, cercetătorul poate renunța la studiul principal care implică resurse logistice mari și, astfel, poate economisi mult timp și bani. [8]
METODE PENTRU CALCULAREA MĂRIMII EȘANTIONULUI
Mărimea eșantionului poate fi calculată folosind metoda intervalului de încredere sau metoda de testare a ipotezelor. În primul, obiectivul principal este de a obține intervale înguste cu fiabilitate ridicată. În aceasta din urmă, ipoteza se referă la testarea dacă estimarea eșantionului este egală cu o anumită valoare specifică.
Ipoteza nulă
Această ipoteză afirmă că nu există nicio diferență între grupul de control și grupul de studiu în raport cu un studiu controlat randomizat (ECA). Respingerea sau respingerea ipotezei nule - și, prin urmare, concluzia că există motive pentru a crede că există o diferență între cele două grupuri, este o sarcină centrală în practica modernă a științei și oferă un criteriu precis pentru respingerea unei ipoteze. [9, 10]
Ipoteză alternativă
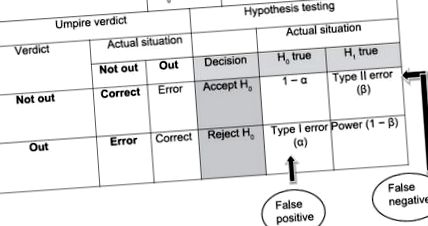
Această ipoteză este contradictorie cu ipoteza nulă, adică presupune că există o diferență între grupuri sau există o oarecare asociere între predictor și rezultat [Figura 1]. [9,10] Uneori, este acceptată prin excludere dacă testul semnificației respinge ipoteza nulă. Poate fi unilaterală (specifică diferența într-o singură direcție) sau față-verso (specifică diferența în ambele direcții).
Posibilități de rezultat în timpul degustării ipotezelor. H 0 - Ipoteză nulă; H 1 - Ipoteza alternativă
Eroarea de tip I (eroare α) apare dacă ipoteza nulă este respinsă atunci când este adevărată. Reprezintă șansa ca cercetătorul să detecteze o diferență între două grupuri atunci când în realitate nu există nicio diferență. Cu alte cuvinte, este șansa unei concluzii fals pozitive. O valoare de 0,05 este cea mai frecvent utilizată.
tabelul 1
Matricea care prezintă modificări ale dimensiunii eșantionului cu dimensiuni variabile de alfa, putere (1-β) și dimensiunea efectului
FORMULE ȘI SOFTWARE
Odată ce acești trei factori sunt fixați, există mai multe moduri (formule, nomogramă, tabele și software) pentru estimarea dimensiunii optime a eșantionului. În prezent, există un număr mare de software disponibile pe internet. Este prudent să vă familiarizați cu instrucțiunile oricărui software pentru a obține dimensiunea eșantionului unui braț al studiului. Poate că cel mai important pas este să verificați cu formula cea mai potrivită pentru a obține o dimensiune corectă a eșantionului. Site-urile web ale unora dintre software-urile utilizate în mod obișnuit sunt furnizate în Tabelul 2. [2,6]
masa 2
Site-uri web pentru unele programe statistice utile
Numărul de formule pentru calcularea dimensiunii și puterii eșantionului, pentru a răspunde cu precizie la diferite modele de studiu și întrebări de cercetare nu este mai mic de 100. Este înțelept să verificați formula adecvată chiar și în timp ce utilizați software-ul. Deși există mai mult de 100 de formule, pentru ECA numărul de formule este limitat. Depinde în esență de măsura principală a rezultatului, cum ar fi media ± SD, rata și proporția. [6] Cititorii interesați pot accesa toate formulele relevante de estimare a dimensiunii eșantionului utilizând linkurile relevante.
Calculul mărimii eșantionului prin compararea a două mijloace
Un studiu pentru a vedea efectul fenilefrinei asupra MAP ca o variabilă continuă după anestezia coloanei vertebrale pentru a contracara hipotensiunea.
MAP ca variabilă continuă:
n = Dimensiunea eșantionului în fiecare grup
μ1 = Media populației în grupul 1 de tratament,
μ2 = Media populației în grupul 2 de tratament
μ1 - μ2 = Diferența pe care investigatorul dorește să o detecteze
℧ = Variația populației (SD)
a = Multiplicator convențional pentru alfa = 0,05,
b = Multiplicator convențional pentru putere = 0,80.
Valoarea a = 1,96, b = 0,842 [Tabelul 3]. Dacă o diferență de 15 mmHg în MAP este considerată între fenilefrină și grupul placebo ca fiind semnificativă clinic (μ1-μ2) și se detectează cu o putere de 80% și un nivel alfa de semnificație de 0,05. [7] n = 2 × ([1,96 + 0,842] 2 × 20 2)/15 2 = 27,9. Asta înseamnă că 28 de subiecți pe grup este mărimea eșantionului.
Tabelul 3
Valorile constante ale Z pentru valorile convenționale α și β
Calculul mărimii eșantionului prin compararea a două proporții
Un studiu pentru a vedea efectul fenilefrinei asupra MAP ca o variabilă binară după anestezia spinării pentru a contracara hipotensiunea.
MAP ca rezultat binar, sub sau peste 60 mmHg (hipotensiune arterială - da/nu):
n = Dimensiunea eșantionului din fiecare grup
p1 = Proporția subiecților cu hipotensiune în grupul de tratament 1
q1 = Proporția subiecților fără hipotensiune în grupul de tratament 1 (1 - p1)
p2 = Proporția subiecților cu hipotensiune în grupul de tratament 2
q2 = Proporția subiecților fără hipotensiune în grupul de tratament 2 (1 - p2)
x = Diferența pe care investigatorul dorește să o detecteze
a = Multiplicator convențional pentru alfa = 0,05
b = Multiplicator convențional pentru putere = 0,8.
Considerând o diferență de 10% ca fiind relevantă din punct de vedere clinic și din publicarea recentă, proporția subiecților cu hipotensiune arterială în grupul tratat va fi de 20% (p1 = 0,2), iar în grupul de control va fi de 30% (p2 = 0,3), și astfel q1 și q2 sunt 0,80 și respectiv 0,70. [7] Presupunând o putere de 80% și un alfa de 0,05, adică 1.96 pentru a și 0.842 pentru b [Tabelul 3] obținem:
([1,96 + 0,842] 2 × [0,20 × 0,80 + 0,30 × 0,70])/0,10 2 = 290,5. Astfel, 291 este dimensiunea eșantionului.
Cercetătorul poate urma unele măsuri, cum ar fi utilizarea variabilelor continue ca rezultat primar, măsurarea precisă a rezultatului sau alegerea rezultatelor care pot fi măsurate corect. Folosirea unui rezultat mai comun, formularea unei ipoteze unilaterale poate ajuta la atingerea acestui obiectiv. Literatura publicată și studiile pilot reprezintă baza calculului dimensiunii eșantionului. Uneori, opiniile experților, experiența personală cu ratele evenimentelor și presupunerea educată devin utile. Variația, dimensiunea efectului sau ratele evenimentelor pot fi subestimate în timpul calculului dimensiunii eșantionului în faza de proiectare. Dacă investigatorul realizează că această subestimare a condus la o „dimensiune prea mică a eșantionului”, recalculul poate fi încercat pe baza datelor intermediare. [15]
REZUMAT
Calculul mărimii eșantionului poate fi ghidat de literatura anterioară, studii pilot și experiențe clinice anterioare. Efortul de colaborare al cercetătorului și al statisticianului este necesar în această etapă. Dimensiunea estimată a eșantionului nu este un adevăr absolut, ci cea mai bună presupunere a noastră. Probleme precum pierderea anticipată de urmărire, analiza subgrupelor mari și proiectele de studiu complicate, necesită o dimensiune mai mare a eșantionului pentru a asigura o putere adecvată pe tot parcursul procesului. O modificare a mărimii eșantionului este proporțională cu varianța (pătratul SD) și invers proporțională cu diferența detectată.
- Plus Size Fitness Healthy Obese
- Îmbrăcăminte de mărime mare ce să îmbraci dacă ești de mărime mare și peste 50 de Gransnet
- Exemplu pentru crearea unui meniu de prânz la restaurant
- Spa-uri de dimensiuni mari care merg la spa-uri ca femeie de dimensiuni mari
- Plus Size Pole Dancing - Tot ce trebuie să știți - Basicinvert78 Un blog Pole Dancer