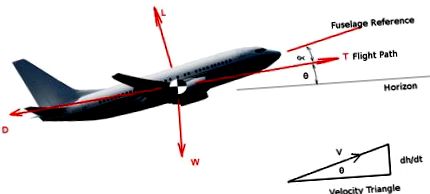
Odată ce aeronava a părăsit solul și a stabilit o urcare constantă de viteză, atunci performanța urcării poate fi calculată pur și simplu utilizând un echilibru al forțelor care acționează asupra vehiculului care urcă.
Se presupune că vehiculul urcă la un unghi constant (θ) și la o viteză constantă înainte (V) cu o rată de urcare de (dh/dt)
Echilibrul forțelor în direcția perpendiculară pe zborul avionului (axa z-vânt) va da:
Echilibrul forțelor în direcția paralelă cu traseul de zbor al aeronavei (axa x-vânt) va da:
Avioanele normale urcă la unghiuri relativ mici, astfel încât unghiul mic presupune că
sin (θ) ≈ θ și cos (θ) ≈ 1 oferă următoarea predicție a unghiului de urcare,
Apoi, observând relația dintre unghiul de urcare, rata de urcare și viteza de zbor,
Utilizarea acestor ecuații într-o schemă numerică este relativ simplă. La o anumită greutate a aeronavei, altitudinii și vitezei de zbor ar trebui să fie posibilă estimarea impulsului curent (T) fiind produsă și Dragul curent (D) (a se vedea secțiunea anterioară privind calculul Împingere și Trage).
Diferența dintre tracțiune și tracțiune la starea de zbor specificată poate fi, prin urmare, utilizată pentru a calcula unghiul de urcare și rata de urcare pentru aeronavă. În mod clar, dacă T = D, atunci avionul nu urcă sau coboară, ci se află în zbor la nivel. De asemenea, o consecință evidentă este că dacă T Coborâre
Coborârea de la altitudine la nivelul mării este o problemă similară dar nu identică de urcat. Este cel mai ușor de analizat analizând un echilibru al forței pentru un decent constant, dar soluția optimă pentru coborâre nu este aceeași cu cea pentru urcare, astfel ecuația va fi utilizată pentru a găsi soluții diferite în această aplicație.
Luarea echilibrului forțelor de-a lungul traseului de zbor oferă,
Luarea echilibrului în unghi drept cu calea de zbor oferă,
Pentru coborâre, obiectivul este de a reduce în primul rând consumul de combustibil și, în același timp, de a maximiza distanța parcursă. Aceasta este o abordare diferită în comparație cu urcarea, unde scopul era optimizarea ratei de urcare. Pentru a minimiza combustibilul, Puterea ar trebui redusă la minimum, deci în acest caz putem presupune T ≈ 0. Pentru a maximiza distanța parcursă, atunci scopul va fi de a avea cel mai mic unghi de coborâre fără împingere, adică pentru a găsi cel mai bun unghiul de alunecare.
Dacă se presupune că unghiul de coborâre este mic atunci $ \ sin (θ) = θ $ și $ \ cos (θ) = 1 $
Prin urmare, optimul pentru coborâre va fi utilizarea unei viteze care maximizează L/D a vehiculului.
- Reducerea greutății aeronavelor și monitorizarea sănătății motorului Știri despre industria aeronautică Știri despre aviație internațională
- Definiții privind greutatea și echilibrul aeronavei
- Clinica Back In Motion pentru alimente și slăbire din Sarasota
- Activa Well Being Slimness (Slabire) - Sănătate cu eliberare imediată; amp; Îngrijire personală - Oaza
- Back Love Handles Best Vitex Fruit Diet Supplement Fată puternică Pastile inteligente de slăbit în oraș