Abstract

fundal

Îmbătrânirea celulară este cel mai bine studiată în drojdia în devenire Saccharomyces cerevisiae. Ca exemplu de trăsătură pleiotropă, durata de viață a drojdiei este influențată de sute de gene interconectate. Cu toate acestea, nu sunt disponibile în prezent metode cantitative pentru a deduce modificări la nivel de sistem în rețelele genetice în timpul îmbătrânirii celulare.

Rezultate

Concluzii

Modelul nostru teoretic oferă o interpretare parsimonieră a datelor experimentale ale duratei de viață din perspectiva rețelelor genetice. Sperăm că munca noastră va stimula un interes mai mare în dezvoltarea modelelor de rețea pentru a studia îmbătrânirea ca trăsătură pleiotropă.

fundal

Înțelegerea îmbătrânirii celulare este esențială pentru înțelegerea noastră asupra îmbătrânirii în general [1]. La nivel molecular, căile despre care se știe că influențează durata de viață joacă adesea funcții importante și conservate în interiorul celulelor [2]. Mecanismele moleculare ale îmbătrânirii celulare sunt cel mai bine înțelese în drojdia în devenire Saccharomyces cerevisiae, un organism model unicelular [3-6]. Efectul de extindere a duratei de viață a sirtuinelor și căilor TOR a fost studiat pe larg în drojdia în devenire și s-a dovedit a fi conservat la alte specii [2, 7-9].

Îmbătrânirea celulelor de drojdie poate fi măsurată prin durata de viață replicativă - numărul de diviziuni celulare pe care celulele le pot realiza înainte de senescență - și durata de viață cronologică - cât timp celulele își pot păstra capacitatea de proliferare în faza staționară [5]. Durata de viață replicativă a celulelor de drojdie este similară cu capacitatea de replicare limitată a celulelor de cultură primară care a fost observată pentru prima dată în celulele umane [10]. Curbele de supraviețuire ale celulelor de drojdie îmbătrânite replicativ sunt în general sigmoidale și pot fi descrise prin modelul Gompertz [11]. Studiile experimentale la nivelul genomului au demonstrat modificări la nivelul rețelei genetice în timpul procesului de îmbătrânire a drojdiei [12]. Îmbătrânirea celulară în drojdie este un proces stocastic, deoarece o populație de celule genotipice omogene poate trăi la vârste diferite. S-a estimat că eritabilitatea generală a duratei de viață replicativă a drojdiei este de aproximativ 22% [11].

În general, îmbătrânirea este definită cantitativ de rata mortalității μ(t), care este rata normală de scădere a viabilității S(t):

Unde t este timpul. Rata mortalitatii μ(t) descrie șansa de a muri peste vârstă și îmbătrânirea apare atunci când rata mortalității este o funcție pozitivă și în creștere a timpului. Rata mortalității este, de asemenea, cunoscută sub numele de forța mortalității, rata eșecului, rata riscului și funcția de intensitate în diferite contexte [13-15]. Rata mortalitatii μ(t) este adesea o funcție exponențială a timpului pentru îmbătrânirea biologică, cunoscută sub numele de modelul Gompertz [16, 17].

În modelul Gompertz, R este rata inițială a mortalității atunci când t este zero și G este coeficientul Gompertz. Rata inițială a mortalității R poate fi interpretat ca potențialul duratei de viață la naștere. Coeficientul Gompertz G are o unitate de 1/timp, descrie accelerarea ratei mortalității μ în timp și, prin urmare, este o măsură pentru rata îmbătrânirii. Având în vedere rolul rețelelor genetice în îmbătrânirea celulară, ar fi informativ să se evalueze modificările rețelei genice în timpul îmbătrânirii drojdiei. Nu este clar modul în care modelul clasic de îmbătrânire Gompertz poate fi folosit pentru a interpreta mecanismele moleculare din datele experimentale de îmbătrânire a drojdiei.

Teoria fiabilității este un domeniu bine stabilit în inginerie [14, 15], iar aplicarea sa în îmbătrânirea biologică a fost recunoscută cu zeci de ani în urmă [18-24]. Murphy a propus un model Bingo în 1978 și a considerat un organism ca o configurație serială a subsistemelor [18]. În mod similar, Skurnick și Kemeny, în 1978, au modelat un organism ca o serie de legături seriale și au recunoscut că cea mai slabă legătură determină vârsta organismului [19]. În 1985, Witten a susținut că un organism poate fi modelat ca un grafic și a explorat modalități de regenerare a modelului Gompertz folosind o configurație serială a componentelor [20]. Gavrilov și Gavrilova au recunoscut importanța componentelor care nu îmbătrânesc și au dezvoltat un model de fiabilitate sofisticat al îmbătrânirii [23, 24]. Toate aceste modele de fiabilitate anterioare se bazează pe subsisteme conectate în serie, analog cu cutiile de siguranțe conectate în serie. Aceste modele anterioare nu au surprins tiparele de interacțiune în rețelele moleculare și, în consecință, nu au devenit instrumente eficiente pentru a sprijini studiile moleculare ale îmbătrânirii, o provocare pe care ne propunem să o abordăm.

În secțiunile următoare, propunem mai întâi un model de rețea parsimonios pentru îmbătrânirea celulară, apoi dezvoltăm o abordare de maximă probabilitate pentru estimarea parametrilor și, în cele din urmă, aplicăm modelul pentru a deduce parametrii rețelei genetice globale din datele replicative ale duratei de viață a drojdiei în devenire. Saccharomyces cerevisiae.

Model

Primul pas în dezvoltarea modelului nostru de rețea genetică pentru îmbătrânirea celulară este modelarea fenotipului morții celulare. Am modificat apoi modelul clasic de fiabilitate al îmbătrânirii într-un model de rețea stocastică.

Modelarea fenotipului morții celulare

estimarea

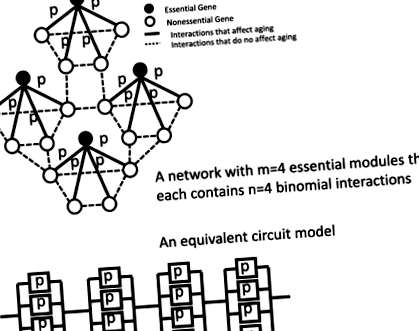
Modelul de rețea de gene parsimonios propus pentru îmbătrânirea celulară. Presupunem că există n numărul de interacțiuni relevante pentru îmbătrânire per nod esențial și că aceste interacțiuni sunt active în celule cu o probabilitate de p la ora zero. Sunt m numărul de noduri esențiale din rețea. Acest model de rețea propus este echivalent cu modelul clasic de bloc de fiabilitate

și rata mortalității modulului esențial, μm este

Dacă ne concentrăm pe durata de viață t ≪ 1 /λ, ecuația de mai sus poate fi simplificată la

În rețelele empirice, cum ar fi rețelele de interacțiune cu proteinele de drojdie, genele/proteinele esențiale interacționează adesea cu multe alte gene. Modelul nostru presupune că, printre aceste interacțiuni, numai n interacțiunile în medie sunt relevante pentru supraviețuirea celulară la ștergerea acestui nod esențial. Cu alte cuvinte, acest model de rețea presupune că, în medie, există n numărul de interacțiuni relevante pentru esențialitatea fiecărui nod esențial. Ne place să subliniem că schimbarea exponențială propusă a forței de interacțiune genetică este o presupunere imperativă pentru o ipoteză nulă. Cu alte cuvinte, susținem că modelele de rețea cu modificări non-exponențiale ale interacțiunilor genetice sunt ipoteze alternative și ar trebui folosite numai atunci când oferă o potrivire semnificativ mai bună la datele experimentale decât modelul de rețea nul cu interacțiuni genice care nu îmbătrânesc.

Un model parsimonios de rețea de gene stocastice pentru îmbătrânirea celulară

Acum putem construi un model de rețea genică stocastic utilizând modulele de rețea esențiale. Presupunem că există m numărul de module esențiale pentru a construi un model de rețea de îmbătrânire ca în Fig. 1. Presupunem că eșecul oricărui modul esențial duce la eșecul întregii rețele și, prin urmare, la moartea celulei. Aceasta este o presupunere rezonabilă, deoarece absența oricărei gene esențiale unice duce la celule de drojdie inviabile [27]. Presupunem că genele esențiale nu interacționează între ele și că eșecurile lor sunt independente. Cu aceste ipoteze, modelul de rețea este echivalent matematic cu construcția în serie a blocurilor din modelul de circuit propus de Gavrilov și Gavrilova [23, 24].

Presupunem că interacțiunile genetice sunt stochastice și că șansa ca o interacțiune genetică să fie activă este p la timp t= 0 (Fig. 1). În rețelele genetice intracelulare, interacțiunile genetice sunt inerent stochastice datorită numărului limitat de produse genetice, zgomotului în expresiile proteinelor și natura aglomerării spațiilor intracelulare [28-30]. Mai mult, zgomotele de transcripție pot fi amplificate în zgomote la niveluri de proteine ​​[31]. Acest model de rețea stocastică este echivalent matematic cu modelul clasic de circuite cu componente binomiale active [24]. Dacă o rețea conține m module esențiale și fiecare genă esențială interacționează stocastic cu n gene neesențiale, bazate pe apendicele C din referința [24], rata mortalității întregii rețele este

si unde c este o constantă de normalizare, \ (c = \ frac> \). Este rezonabil să aproximăm rata modulară a mortalității ca o însumare a posibilelor modele de conexiune în ecuație. 6 dacă ne concentrăm pe gama de durate de viață t ≪ 1 /λ [24, 32]. Termenul de însumare în ec. 6 este formula binomială [(1−p)+pλt] n−1, ceea ce duce la următoarele reamenajări:

Parametrul t0 are unitatea de timp și se numește vârsta virtuală inițială a sistemului (IVAS). Parametrul R este echivalent cu rata inițială a mortalității în modelul clasic Gompertz [23, 24].

Funcția de mortalitate cu trei parametri în ecuație. 8 poate fi utilizat pentru a se potrivi unui set de date experimentale cu durata de viață, care poate fi dezvăluit t0 (durata de viață virtuală inițială) și n (numărul de interacțiuni care influențează durata de viață per nod esențial).

Funcția de supraviețuire a rețelei bazată pe funcția de mortalitate în ecuație. 8 se găsește a fi

iar funcția densității probabilității îmbătrânirii rețelei este

Maximul probabilității transformate în jurnal sumat pe întregul set de date experimentale va produce estimări ale parametrilor modelului. Am implementat aceste proceduri numerice în codurile R.

Având în vedere ipotezele noastre simple, este important să testăm utilitatea acestui model parsimonios propus pentru îmbătrânirea celulară. Prin urmare, am aplicat acest model de rețea de îmbătrânire celulară la îmbătrânirea replicativă a drojdiei în devenire datorită disponibilității multor seturi de date experimentale obținute în condiții controlate. Vă sugerăm ca valoarea estimată n din seturile de date experimentale privind durata de viață pot fi denumite numărul mediu aparent de interacțiuni care influențează durata de viață pe nod esențial.

rezultate si discutii

Aplicare la mutanți de drojdie cu efecte cunoscute asupra duratei de viață replicative

Pentru a demonstra în continuare utilitatea modelului nostru propus, l-am aplicat la măsurători experimentale replicative ale duratei vieții mutanților de drojdie cu efecte cunoscute asupra îmbătrânirii [33]. Am estimat parametrii modelului din durata de viață replicativă utilizând metode de maximă probabilitate. Duratele de viață replicative au fost inițiate pentru a atenua potențialele erori de constatare.

SIR2 este o deacetilază dependentă de NAD implicată în amortizarea cromozomilor, segregarea cromozomilor și recombinarea ADN-ului. Ștergerea SIR2 scurtează durata de viață replicativă a drojdiei și supraexprimarea SIR2 îl extinde [33, 34]. Așa cum se arată în Tabelul 1, rezultatele noastre de montare a modelului arată o scădere drastică t0 estimare în domnule2 Δ —Mutantul de ștergere a SIR2 și moderat crescut t0 estimare în SIR2OX—Mutantul supraexprimat al SIR2 în comparație cu controlul de tip sălbatic BY4742. Pe baza ecuației. 9, t0 este invers asociat cu rata de descompunere a interacțiunii λ. Valori mai mici ale λ indică o mai mare fiabilitate a interacțiunilor proteice. Prin urmare, valoarea scăzută a t0 sugerează că ștergerea SIR2 scade fiabilitatea interacțiunilor genetice, în timp ce supraexprimarea SIR2 îl mărește.

Au fost studiați și mutanți ai altor două gene de drojdie. FOB1 reglează numărul de copii ale ADNc în celulele de drojdie, iar ștergerea acestuia extinde durata de viață replicativă a drojdiei [33]. HXK2, o hexokinază, limitează aportul de glucoză pentru glicoliză, iar mutantul său de deleție este considerat un model genetic pentru restricția calorică [33]. Rezultatele noastre arată că în ambii mutanți cu o singură deleție FOB1 și HXK2, estimări ale t0 creștere și estimări ale n rămân în același interval. În mutanții cu dublă ștergere în care ambii FOB1 și HXK2 sunt absente, t0 crește cu cele mai mari valori medii, deși n scade moderat.

După cum se arată în Tabelul 1, am constatat că IVAS estimat t0 este în general mult mai mare decât durata medie de viață a acestor tulpini de drojdie. În toate tulpinile studiate, tendințele acestor modificări au rămas atunci când am inițiat măsurătorile experimentale, indicând aceste modificări ale t0 sunt robuste la fluctuațiile de constatare în timpul experimentelor replicative pe durata vieții.

Când t ≪ t0, rata de mortalitate a rețelei binomiale μNu va aborda modelul clasic de îmbătrânire cu doi parametri Gompertz [24] și coeficientul Gompertz, G, se găsește a fi

Prin urmare, modelul de rețea propus pentru îmbătrânire poate fi privit ca o extensie a modelului Gompertz cu doi parametri și oferă un model alternativ de utilizat în examinarea îmbătrânirii celulare.

În concordanță cu opinia noastră conform căreia modelul propus este o extensie a modelului Gompertz, modelul de îmbătrânire a rețelei propus este similar cu modelul Gompertz în timpul montării pe baza criteriului informației Akaike (AIC) (tabelul 1). Intervalele AIC estimate folosind modelul de rețea se suprapun în cea mai mare parte cu cele care utilizează modelul Gompertz. Aceste observații au fost susținute în continuare de suprapunerea curbelor de densitate de montare peste histogramele duratei de viață în aceste tulpini de drojdie (Fig. 2). În general, când modelul de îmbătrânire Gompertz este potrivit pentru durata de viață experimentală - cum ar fi pentru tipul sălbatic BY4742, mutanții de ștergere domnule2Δ,hxk2Δ, și fob1Δ—Modelul de îmbătrânire a rețelei propus este, de asemenea, o potrivire rezonabilă. Când distribuția duratei de viață devine înclinată în mutantul supraexprimat SIR2OX, atât modelul Gompertz, cât și modelul binomial devin problematice.

Suprapunerea curbelor de potrivire cu histograme de durată de viață la mutanții de drojdie. Curbele de montare roșie reprezintă forma binomială a modelului de îmbătrânire a rețelei, iar curbele de montare albastră reprezintă modelul Gompertz cu doi parametri. A BY4742. b fob1Δ. c hxk2Δ. d fob1Δhxk2Δ. e domnule2Δ. f SIR2BOU

Atunci când se aplică acest model simplu parsimonios pentru a analiza datele experimentale, vă sugerăm că valoarea estimată n, numit numărul mediu aparent de interacțiuni care influențează durata de viață pe nod esențial, este similar cu alte concepte teoretice, cum ar fi dimensiunea efectivă a populației în genetica populației. Mărimea efectivă a populației, deși adesea drastic mai mică decât dimensiunea aparentă a populațiilor biologice, ne poate ajuta să evaluăm diferite modele din genetică populației. Un alt exemplu este rata eficientă de transmitere a virusurilor în epidemiologie. În practică, utilitatea modelului de îmbătrânire a rețelei propus constă în capacitatea sa de a ajuta la evaluarea modificărilor potențiale ale rețelei genetice din rezultatele experimentale ale vieții. În consecință, dezvoltăm în prezent abordări de testare a modelelor imbricate bazate pe probabilități pentru a compara parametrii modelului de îmbătrânire a rețelei din diferite experimente.

În plus, modelul nostru de rețea oferă perspective interesante asupra îmbătrânirii fagilor bacterieni [25]. Când G se apropie de zero, valoarea lui t0 abordează infinit pe baza ecuației. 13, care la rândul său sugerează că valoarea lui λ se apropie de zero pe baza ecuației. 9. O valoare extrem de mică a λ-Rata de degradare a interacțiunii genetice indică faptul că puterea interacțiunilor genetice poate rămâne puternică pentru o perioadă foarte lungă de timp în timpul îmbătrânirii. Prin urmare, modelul nostru de rețea prezice că puterea interacțiunii genice este extrem de fiabilă în fagii bacterieni.

Aplicarea în izolate sălbatice de drojdie și implicația pentru corelația streher-Muldivan

Am aplicat modelul de rețea propus de îmbătrânire celulară folosind seturi de date replicative ale vieții izolate sălbatice de Saccharomyces cerevisiae [11]. Așa cum se arată în Tabelul 2, intervalele de valori AIC pentru modelul de rețea se suprapun în general pe cele pentru modelul Gompertz, în concordanță cu constatările noastre folosind tulpinile de laborator. Am constatat că IVAS estimat (t0) este între 30,6 și 74,0 cu o valoare medie de 45,4 în colecția noastră de izolate de drojdie sălbatică, care se află în același interval de BY4742 (t0 = 56,2). Estimat n este între 6,1 și 8,0 cu o valoare medie de 7,0, ușor mai mică decât cele estimate în fundalul tulpinii de laborator.

Am constatat că presupunerea t ≪ 1 /λ poate fi îndeplinit în mod rezonabil. Dacă presupunem activarea interacțiunii genice cu p= 0,7, intervalul 1 /λ este de 73–173 diviziuni celulare cu o medie de 106. Dacă presupunem p= 0,9, intervalul 1 /λ este 283-666 diviziuni celulare cu o medie de 408. Durata medie de viață replicativă a acestor izolate naturale este de 31. Prin urmare, aceste rezultate confirmă că ipoteza de t ≪ 1 /λ pentru abordarea noastră de modelare poate fi îndeplinită atâta timp cât probabilitatea de activare a interacțiunii p este mai mare de 0,5. Cu alte cuvinte, eterogenitatea rețelei genetice ar trebui să fie moderată. Pentru rețelele genelor/proteinelor de drojdie cu peste o mie de gene esențiale, starea de t ≪ 1 /λ indică faptul că atunci când o celulă moare la vârsta de t datorită unui modul esențial deosebit de slab, interacțiunile genetice rămase rămân în mare măsură funcționale.

Rolul potențial de mediator al t0 în corelația Strehler-Mildvan în izolatele naturale de drojdie. A Corelația Strehler-Mildvan în izolatele naturale studiate de drojdie. Dimensiunea fiecărui punct de date reprezintă valoarea lui t0. b O corelație pozitivă între Buturuga10R și t0. Mărimea fiecărui punct de date reprezintă valoarea lui G. Testele de mediere arată că t0 mediază corelația dintre Buturuga10R și G

Concluzii

Prezentăm un model probabilistic de rețea genică de îmbătrânire celulară care poate servi drept model parsimonios pentru interpretarea măsurătorii duratei de viață experimentale. Modelul nostru de îmbătrânire a rețelei convertește coeficientul clasic Gompertz în doi parametri: n (numărul mediu de interacțiuni care influențează durata de viață per nod esențial) și t0 (vârsta virtuală inițială). Parametrul n este informativ cu privire la configurarea rețelei și parametrul t0 este informativ cu privire la fiabilitatea interacțiunii și heterogenitatea rețelei. Aplicațiile modelului nostru pentru îmbătrânirea drojdiei au arătat că modelul nostru este la fel de aplicabil ca modelul clasic cu doi parametri Gompertz. În general, am arătat că modelul de îmbătrânire în rețea propus poate ajuta la studiul molecular al îmbătrânirii celulare. Având în vedere natura pleiotropică a îmbătrânirii, sperăm că această lucrare poate stimula un interes mai mare în dezvoltarea unor modele de rețea mai sofisticate pentru studiul îmbătrânirii.