Dacă am o mașină (cu un anumit motor) optimizată (în funcție de distribuție și formă și greutate) pentru a atinge viteza maximă posibilă și pun acel motor într-o mașină care este mai grea (dar altfel aceeași formă și design), mașinile mai grele au aceeași viteză maximă în lumea reală?

Presupun că mașina mai grea va accelera într-un ritm mai lent, dar nu sunt sigur dacă în cele din urmă va atinge aceeași viteză maximă ca și mașina mai ușoară. Factori precum rezistența la aer și modul în care mașinile de curse sunt concepute pentru a îmbrățișa solul (așa cum înțeleg eu) le-ar putea determina să nu aibă aceeași viteză maximă?

Dacă nu au aceeași viteză maximă, ar fi posibil să reproiectați mașina mai grea (adică să-i schimbați forma și distribuția greutății) astfel încât să aibă aceeași viteză maximă ca (sau o viteză maximă mai mare decât) bricheta mașină? Gândul meu este că, dacă mașina mai grea nu trebuie să utilizeze rezistența aerului pentru a „îmbrățișa solul”, atunci ar putea fi proiectată mai aerodinamic?

Actualizare 1

Bine, $ F_ $ crește cu $ m $, care scade $ | v | _ $. Are sens.

Dar oare mașina mai grea ar putea merge la fel de repede sau mai repede cu un alt design? Iată raționamentul meu:

  1. Viteza crește în timp ce $ F_ $ al mașinii este mai mare decât $ F_ + F_ $ al fricțiunii .
  2. $ F_ $ crește pe măsură ce crește $ | v | $.
  3. „Aripile cu capul în jos” sunt folosite pentru a oferi $ F_ $ suplimentar (să-i spunem $ F_ $).
  4. A avea prea puțin $ F_ $ scade $ F_ $ .
  5. „Aripi” mai mari în # 3 măresc $ F_ $, dar crește și $ F_ $
  6. $ F_ = F_ + F_ $

Pe baza acestei logici, o mașină mai ușoară va avea nevoie de „aripi” mai mari (# 6) pentru a menține tracțiunea (# 3) pentru a menține viteza (# 4), dar creșterea $ F_ $ crește $ F_ $ cu # 5, ceea ce scade $ | v | _ $ (# 1 + # 2). Cu toate acestea, pe măsură ce $ m $ crește, $ F_ $ crește, prin urmare este nevoie de mai puțin $ F_ $ (# 6) și, prin urmare, se experimentează mai puțin $ F_ $. Deci avem

  • mașina mai grea ar avea $ F_ $ mai mare, care scade $ | v | _ $ cu o sumă constantă
  • mașina mai ușoară ar avea $ F_ $ mai mare, care crește pe măsură ce crește $ | v | $

Deci, urmând acest raționament, nu ar fi posibil să construim o mașină mai grea, care să aibă mai mult de $ | v | _ $ decât o mașină mai ușoară?

Actualizare 2

Clarificare: # 4 ar trebui să însemne „când există prea puțină forță care împinge mașina în jos, roțile vor aluneca, ceea ce reduce cantitatea de forță pe care o poate oferi motorul”. Este corect?

2 Răspunsuri 2

Problema pe care ați formulat-o este că aceste două mașini sunt identice în afară de diferența de masă, așa că haideți să o limităm doar la două mașini identice în care una are o greutate suplimentară. Mașina mai grea va accelera mai lent, bazat pe $ F = ma $ simplu, unde $ F $ este același, deci $ a $ trebuie să fie mai mic pentru un $ m $ mai mare. Fricțiunea, care determină viteza maximă împreună cu forța, este puțin mai dezordonată.

Rezistența la aer este practic afectată doar de forma mașinii, deci va fi complet neschimbată. Cu toate acestea, mașina mai grea va avea o frecare mai mare la sol la contactul dintre roți și șosea și, din acest motiv, va avea o viteză maximă mai mică. O modalitate prin care vă puteți convinge că fricțiunea anvelopei depinde de greutatea mașinii este să considerați doar că anvelopa se deformează și creează căldură, iar o masă mai mare îl va determina să se deformeze mai mult la fiecare viraj. Pentru mașinile super rapide fricțiunea anvelopelor este de fapt extrem de semnificativă.

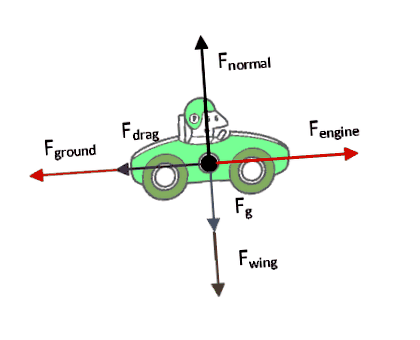
Datorită formalismului sporit prin întrebare, pot oferi un pic mai multe detalii. Iată o diagramă de forță cu adevărat de bază pe care am făcut-o pentru asta. Nu este perfect, dar cred că este suficient. Și după logica întrebării, $ F_ $ este împărțit în 2 părți în care una este din corp și una este din aripă. Mai mult, forțele aerodinamice ale aripii sunt într-adevăr forța specifică vântului plus $ F_ $ .

fluidelor

Deci, vorbeam despre creșterea greutății mașinii. Aceasta crește $ F_g $ și $ F_ $ deoarece în viața reală forța de frecare a roții are o dependență semnificativă de greutate. Întrebarea a menționat necesitatea aripii pentru a menține tracțiunea. Deci, tracțiunea este un punct dificil, deoarece este legată de greutate.

Cred că dacă ar fi nevoie de o anumită rază de viraj fără alunecare pentru o mașină de curse, această cantitate ar trebui să fie menținută constantă. Cred că acest lucru ajunge puțin la ceea ce dorea întrebarea, care este că dacă masa, $ M $, s-ar schimba, ar fi necesară o reproiectare pentru a menține aceeași tracțiune (a se vedea ecuația de mai sus).

După cum o văd, mașina mai grea va avea o viteză maximă mai mare. Iata de ce:

Viteza maximă apare atunci când forțele care împing mașina înainte (puterea motorului) sunt egale cu forțele care țin mașina înapoi (rezistență aerodinamică, rezistență la rulare).

Dacă luați două mașini identice, dar creșteți masa unei mașini, acestea vor avea aceeași putere a motorului, aceeași rezistență aerodinamică și aceeași rezistență la rulare (a se vedea nota 1 de mai jos). Singurul lucru care are modificări este masa și, deoarece masa nu este un factor în determinarea vitezei maxime, deci viteza maximă ar trebui să rămână aceeași.

Acum pot părea că mă contrazic. La urma urmei, la start, am spus că mașina mai grea va avea o viteză maximă mai mare, dar acum spun că vor fi la fel. Asta pentru că aici există de fapt un alt element. Inerția mașinii împinge și ea mașina înainte. Deci, ecuația reală este următoarea:

Viteza maximă apare atunci când forțele care împing mașina înainte (puterea motorului, inerția mașinii) sunt egale cu forțele care țin mașina înapoi (rezistență aerodinamică, rezistență la rulare).

Inerția unei mașini poate fi definită prin următoarea ecuație: $$ I = \ frac12mv ^ 2 $$ unde $ I $ este inerția mașinii, $ m $ este masa mașinii și $ v $ este viteza mașinii (viteza).

Deci, în cele din urmă, inerția crește odată cu creșterea masei. Poate face acest lucru în cantități mici, dar totuși crește. Deoarece inerția mașinii este una dintre forțele care împing mașina înainte, creșterea inerției va crește viteza maximă. Deoarece creșterea masei crește inerția, creșterea masei va crește viteza maximă.

Nota 1: Din punct de vedere tehnic, rezistența la rulare crește odată cu masa, deoarece există o greutate mai mare pe fiecare anvelopă. Cu toate acestea, acest lucru poate fi compensat prin ajustarea presiunilor anvelopelor, deci este irelevant. Există, de asemenea, o greutate mai mare pe rulmenții roților, dar piesele sunt proiectate suficient de bine acum, deoarece rezistența la adăugarea greutății este minimă și poate fi ignorată.