În acest tutorial, vom afla despre una dintre cerințele de bază ale electronicii digitale, adică codurile binare sau sistemul de numere binare.
Cuprins
Introducere
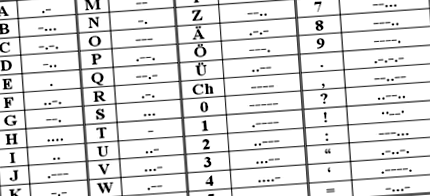
Primul sistem de comunicare electrică de succes a fost telegraful, care a fost inventat de Samuel F.B. Morse în anul 1832. Operatorii de telegraf au folosit un cod de clicuri pentru a trimite mesajele. Dacă tasta este apăsată pentru o perioadă scurtă de timp, este codul Morse numit „punct” și dacă tasta apăsată pentru o lungă perioadă de timp este „Dash”. Un exemplu de cod Morse este prezentat mai jos:
Dacă se observă logic, se pot scrie diverse combinații nenumărate de puncte și liniuțe de orice fel de cuvinte (chiar propoziții) folosind codul de mai sus. În aceleași cifre binare, de asemenea, să fie utilizate pentru a face astfel de combinații nenumărate. Acestea pot fi considerate coduri binare.
Altele decât codul 8421 sau codul BCD, codul 2421, codul 5211, codul reflectorizant, codul secvențial, codul neponderat, codul excee-3 și codul gri sunt câteva dintre codurile care au fost popularizate.
Coduri binare utilizate în mod obișnuit
Înainte de a intra în detaliile codurilor binare individuale, să analizăm rapid unele dintre codurile binare utilizate în mod obișnuit. Următoarea este lista:
- 8421 Coduri
- 2421 Coduri
- 5211 Coduri
- Exces-3 Coduri
- Coduri gri
În lista de mai sus, primele trei adică 8421, 2421 și 5211 sunt coduri ponderate, în timp ce celelalte două sunt coduri binare neponderate.
Sisteme binare ponderate
Valorile atribuite locurilor consecutive în sistemul zecimal care este un sistem de valori de poziție sunt 10⁴, 10³, 10², 10¹, 10⁰, 10⁻¹, 10⁻², 10⁻³ ... de la stânga la dreapta. Este ușor de înțeles că greutatea cifrei sistemului zecimal este „10”.
De exemplu (3546.25) ₁₀ = 3 x 10³ + 5 x 10² + 4 x 10¹ + 6 x 10⁰ + 2 x 10⁻¹ + 5 x 10⁻²
În același mod, valorile atribuite locurilor consecutive în sistemul binar, care este, de asemenea, un sistem de valori de poziție, dar numit ca sistem binar ponderat sunt 2⁴, 2³, 2², 2¹, 2⁰, 2⁻¹, 2⁻², 2 ⁻³ ... De la stânga la dreapta. Este ușor de înțeles că greutatea cifrei sistemului binar este „2”.
De exemplu: (1110110) ₂ = 1 x 2⁶ + 1 x 2⁵ + 1 x 2⁴ + 0 x 2³ + 1 x 2² + 1 x 2¹ + 0 x 2⁰
= 64 + 32 + 16 + 0 + 4 + 2 + 0 = (118) 10
Greutăți binare
Ori de câte ori apare un număr binar, echivalentul său zecimal poate fi găsit cu ușurință după cum urmează.
- Când este 1 într-o poziție de cifră, trebuie adăugată greutatea acelei poziții.
- Când există 0 într-o poziție de cifră, greutatea acelei poziții nu trebuie luată în considerare.
De exemplu, numărul binar 1100 are un echivalent zecimal de 8 + 4 + 0 + 0 = 12.
Cod 8421 sau Cod BCD
Numerele zecimale 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 pot fi exprimate în numere binare așa cum se arată mai jos. Toate aceste numere binare exprimate din nou în ultima coloană prin extinderea în 4 biți. Conform cifrelor binare ponderate, numerele binare de 4 biți pot fi exprimate în funcție de valoarea lor locală de la stânga la dreapta ca 8421 (2³ 2² 2¹ 2⁰ = 8421).
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 10 | 0010 |
| 3 | 11 | 0011 |
| 4 | 100 | 0100 |
| 5 | 101 | 0101 |
| 6 | 110 | 0110 |
| 7 | 111 | 0111 |
| 8 | 1000 | 1000 |
| 9 | 1001 | 1001 |
Conform expresiei de mai sus, toate numerele zecimale scrise în codul binar de 4 biți sub forma 8421 și aceasta se numește cod 8421 și, de asemenea, ca cod binar zecimal BCD.
Deoarece acesta este un cod drept, orice număr zecimal poate fi exprimat cu ușurință, deoarece greutățile pozițiilor sunt drepte pentru o conversie ușoară în acest cod 8421.
Există și alte forme de coduri care nu sunt atât de populare, ci mai degrabă confuze. Acestea sunt codul 2421, codul 5211, codul reflectorizant, codul secvențial, codul neponderat, codul exces-3 și codul gri. Ei au propria lor importanță pentru unele dintre aplicațiile exclusive și pot fi utile pentru unele dintre aplicațiile tipice.
2421 Cod
Acest cod este, de asemenea, un cod de aplicație de 4 biți în care greutățile binare poartă 2, 4, 2, 1 de la stânga la dreapta.
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 10 | 0010 |
| 3 | 11 | 0011 |
| 4 | 100 | 0100 |
| 5 | 101 | 1011 |
| 6 | 110 | 1100 |
| 7 | 111 | 1101 |
| 8 | 1000 | 1110 |
| 9 | 1001 | 1111 |
Codul 5211
Acest cod este, de asemenea, un cod de aplicație de 4 biți în care greutățile binare transportă 5, 4, 2, 1 de la stânga la dreapta.
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 10 | 0011 |
| 3 | 11 | 0101 |
| 4 | 100 | 0111 |
| 5 | 101 | 1000 |
| 6 | 110 | 1010 |
| 7 | 111 | 1100 |
| 8 | 1000 | 1110 |
| 9 | 1001 | 1111 |
Cod reflectorizant
Se poate observa că în codurile 2421 și 5211, codul pentru zecimalul 9 este complementul codului pentru zecimal 0, codul pentru zecimalul 8 este complementul codului pentru zecimalul 1, codul pentru zecimalul 7 este complementul din codul pentru zecimala 2, codul pentru zecimala 6 este complementul codului pentru zecimala 3, codul pentru zecimala 5 este complementul codului pentru zecimala 4, aceste coduri sunt numite coduri reflexive. Același lucru poate fi observat în următorul tabel:
- 32-6-28 - Permise pentru excesul de greutate și dimensiuni 2010 Cod Georgia Coduri și Statute SUA Legea SUA
- Coduri promoționale pentru dietă de 2 zile (reducere de 45%) Cod promoțional 2020
- Cel mai bun sistem suplimentar pentru arderea caloriilor, grăsimilor, construirii musculaturii
- Cele mai bune moduri de a curăța; Curățați sistemul dvs. Teami
- 10 alimente care vă stimulează sistemul imunitar - San Antonio Integrated Healthcare