Analiza de regresie este o tehnică utilizată pe scară largă, care este utilă pentru multe aplicații. Introducem tehnica aici și extindem utilizările sale în modulele ulterioare.

Regresie liniară simplă

Regresia liniară simplă este o tehnică adecvată pentru a înțelege asocierea dintre o variabilă independentă (sau predictivă) și o variabilă continuă dependentă (sau rezultată). De exemplu, să presupunem că dorim să evaluăm asocierea dintre colesterolul total (în miligrame pe decilitru, mg/dL) și indicele de masă corporală (IMC, măsurat ca raportul dintre greutatea în kilograme și înălțimea în metri 2) în care colesterolul total este variabilă dependentă, iar IMC este variabila independentă. În analiza de regresie, variabila dependentă este notată Y și variabila independentă este notată X. Deci, în acest caz, Y = colesterol total și X = IMC.

Atunci când există o singură variabilă dependentă continuă și o singură variabilă independentă, analiza se numește o analiză de regresie liniară simplă. Această analiză presupune că există o asociere liniară între cele două variabile. (Dacă se presupune o altă relație, cum ar fi o relație curbiliniară sau exponențială, se efectuează analize de regresie alternative.)

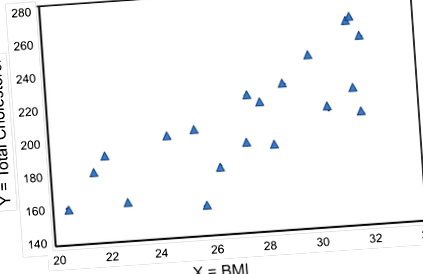
Figura de mai jos este o diagramă scatter care ilustrează relația dintre IMC și colesterolul total. Fiecare punct reprezintă perechea observată (x, y), în acest caz, IMC și colesterolul total corespunzător măsurat la fiecare participant. Rețineți că variabila independentă (IMC) este pe axa orizontală și variabila dependentă (colesterolul seric total) pe axa verticală.

IMC și colesterol total

variabila independentă

Graficul arată că există o asociere pozitivă sau directă între IMC și colesterolul total; participanții cu IMC mai mic sunt mai predispuși să aibă niveluri mai scăzute de colesterol total și participanții cu IMC mai mari să aibă niveluri mai ridicate de colesterol total. În contrast, să presupunem că examinăm asocierea dintre IMC și colesterol HDL.

În contrast, graficul de mai jos prezintă relația dintre IMC și HDL colesterol în același eșantion de n = 20 de participanți.

IMC și HDL colesterol

Acest grafic arată o asociere negativă sau inversă între IMC și colesterol HDL, adică cei cu IMC mai mic au un nivel mai ridicat de colesterol HDL, iar cei cu IMC mai mare au un nivel mai scăzut de colesterol HDL.

Pentru oricare dintre aceste relații am putea folosi o analiză de regresie liniară simplă pentru a estima ecuația liniei care descrie cel mai bine asocierea dintre variabila independentă și variabila dependentă. Ecuația de regresie liniară simplă este următoarea:

Unde Da este valoarea prezisă sau așteptată a rezultatului, X este predictorul, b0 este interceptarea Y estimată și b1 este panta estimată. Intercepția Y și panta sunt estimate din datele eșantionului și sunt valorile care minimizează suma diferențelor pătrate dintre valorile observate și cele prezise ale rezultatului, adică estimările reduc:

Aceste diferențe între valorile observate și prezise ale rezultatului sunt numite reziduuri . Estimările interceptării Y și ale pantei minimizează suma reziduurilor pătrate și se numesc estimări ale celor mai mici pătrate . 1

Conceptual, dacă valorile lui X ar furniza o predicție perfectă a lui Y atunci suma diferențelor pătrate între valorile observate și cele prezise ale lui Y ar fi 0. Asta ar însemna că variabilitatea în Y ar putea fi complet explicată prin diferențe în X. Cu toate acestea, dacă diferențele dintre valorile observate și cele prezise nu sunt 0, atunci nu suntem în măsură să explicăm în totalitate diferențele în Y pe baza lui X, atunci există erori reziduale în predicție. Eroarea reziduală ar putea rezulta din măsurători inexacte ale lui X sau Y sau ar putea exista și alte variabile în afară de X care afectează valoarea lui Y.

Pe baza datelor observate, cea mai bună estimare a unei relații liniare va fi obținută dintr-o ecuație pentru linia care minimizează diferențele dintre valorile observate și prezise ale rezultatului. Interceptare Y. din această linie este valoarea variabilei dependente (Y) atunci când variabila independentă (X) este zero. pantă din linie este modificarea variabilei dependente (Y) în raport cu o schimbare de o unitate în variabila independentă (X). Estimările celor mai mici pătrate ale interceptării y și ale pantei sunt calculate după cum urmează:

  • r este coeficientul de corelație a eșantionului,
  • eșantionul înseamnă și
  • și Sx și Sy sunt abaterile standard ale variabilei independente x și respectiv variabilei dependente y.

IMC și colesterol total

Estimările celor mai mici pătrate ale coeficienților de regresie, b 0 și b1, care descriu relația dintre IMC și colesterolul total sunt b0 = 28,07 și b1 = 6,49. Acestea sunt calculate după cum urmează:

Estimarea interceptării Y (b0 = 28,07) reprezintă nivelul total estimat de colesterol atunci când IMC este zero. Deoarece un IMC zero nu are sens, interceptarea Y nu este informativă. Estimarea pantei (b1 = 6,49) reprezintă modificarea colesterolului total față de o modificare a unității în IMC. De exemplu, dacă comparăm doi participanți ale căror IMC diferă cu 1 unitate, ne-am aștepta ca colesterolii lor total să difere cu aproximativ 6,49 unități (persoana cu IMC mai mare având colesterolul total mai mare).

Ecuația liniei de regresie este după cum urmează:

Graficul de mai jos prezintă linia de regresie estimată suprapusă pe diagrama scatter.

Ecuația de regresie poate fi utilizată pentru a estima colesterolul total al unui participant în funcție de IMC-ul acestuia. De exemplu, să presupunem că un participant are un IMC de 25. Am estima colesterolul lor total la 28,07 + 6,49 (25) = 190,32. Ecuația poate fi, de asemenea, utilizată pentru a estima colesterolul total pentru alte valori ale IMC. Cu toate acestea, ecuația ar trebui utilizată numai pentru a estima nivelurile de colesterol pentru persoanele ale căror IMC se află în intervalul de date utilizate pentru a genera ecuația de regresie. În eșantionul nostru, IMC variază de la 20 la 32, astfel ecuația ar trebui utilizată numai pentru a genera estimări ale colesterolului total pentru persoanele cu IMC în acest interval.

Există teste statistice care pot fi efectuate pentru a evalua dacă coeficienții de regresie estimați (b0 și b1) sunt diferiți semnificativ statistic de zero. Testul cel mai interesant este de obicei H0: b1 = 0 versus H1: b1 ≠ 0, unde b1 este panta populației. Dacă panta populației este semnificativ diferită de zero, concluzionăm că există o asociere semnificativă statistic între variabilele independente și dependente.

IMC și HDL colesterol

Estimările celor mai mici pătrate ale coeficienților de regresie, b0 și b1, care descriu relația dintre IMC și colesterol HDL sunt după cum urmează: b0 = 111,77 și b1 = -2,35. Acestea sunt calculate după cum urmează:

Din nou, interceptarea Y este neinformativă, deoarece un IMC zero nu are sens. Estimarea pantei (b1 = -2,35) reprezintă modificarea colesterolului HDL în raport cu o modificare a unității în IMC. Dacă comparăm doi participanți ale căror IMC diferă cu 1 unitate, ne-am aștepta ca colesterolii lor HDL să difere cu aproximativ 2,35 unități (cu persoana cu IMC mai mare având colesterolul HDL mai mic. Figura de mai jos arată linia de regresie suprapusă pe diagrama scatter pentru IMC și colesterol HDL.

Analiza de regresie liniară se bazează pe presupunerea că variabila dependentă este continuă și că distribuția variabilei dependente (Y) la fiecare valoare a variabilei independente (X) este distribuită aproximativ în mod normal. Rețineți, totuși, că variabila independentă poate fi continuă (de exemplu, IMC) sau poate fi dihotomică (a se vedea mai jos).

Școala de sănătate publică a Universității din Boston
SoftChalk 9.02.10