Teoria moleculară cinetică

Observațiile experimentale despre comportamentul gazelor discutate până acum pot fi explicate cu un model teoretic simplu cunoscut sub numele de teoria moleculară cinetică. Această teorie se bazează pe următoarele postulate sau presupuneri.

  1. Gazele sunt compuse dintr-un număr mare de particule care se comportă ca niște obiecte sferice dure într-o stare de mișcare constantă, aleatorie.
  2. Aceste particule se mișcă în linie dreaptă până când se ciocnesc cu o altă particulă sau cu pereții containerului.
  3. Aceste particule sunt mult mai mici decât distanța dintre particule. Prin urmare, cea mai mare parte a volumului unui gaz este spațiu gol.
  4. Nu există nici o forță de atracție între particulele de gaz sau între particule și pereții containerului.
  5. Coliziunile dintre particulele de gaz sau coliziunile cu pereții containerului sunt perfect elastice. Nimic din energia unei particule de gaz nu se pierde atunci când se ciocnește cu o altă particulă sau cu pereții containerului.
  6. Energia cinetică medie a unei colecții de particule de gaz depinde de temperatura gazului și de nimic altceva.

Ipotezele din spatele teoriei moleculare cinetice pot fi ilustrate cu aparatul prezentat în figura de mai jos, care constă dintr-o placă de sticlă înconjurată de pereți montați deasupra a trei motoare vibrante. O mână de rulmenți cu bile de oțel sunt așezați deasupra plăcii de sticlă pentru a reprezenta particulele de gaz.

cinetică

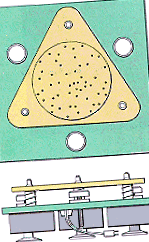Când motoarele sunt pornite, placa de sticlă vibrează, ceea ce face ca rulmenții cu bile să se miște în mod constant, aleatoriu (postulatul 1). Fiecare bilă se mișcă în linie dreaptă până se ciocnește cu o altă bilă sau cu pereții containerului (postulatul 2). Deși ciocnirile sunt frecvente, distanța medie între rulmenții cu bile este mult mai mare decât diametrul bilelor (postulatul 3). Nu există o forță de atracție între rulmenții cu bile sau între rulmenții cu bile și pereții containerului (postulatul 4).

Coliziunile care apar în acest aparat sunt foarte diferite de cele care apar atunci când o minge de cauciuc este aruncată pe podea. Coliziunile dintre bila de cauciuc și podea sunt inelastice, așa cum se arată în figura de mai jos. O porțiune din energia mingii se pierde de fiecare dată când lovește podeaua, până când se rostogolește în cele din urmă. În acest aparat, coliziunile sunt perfect elastice. Bilele au la fel de multă energie după o coliziune ca înainte (postulatul 5).

Orice obiect în mișcare are o energie kinetică care este definit ca jumătate din produsul din masa sa de ori viteza pătrată.

În orice moment, unii dintre rulmenții cu bile de pe acest aparat se mișcă mai repede decât alții, dar sistemul poate fi descris printr-o energie cinetică medie. Când creștem „temperatura” sistemului prin creșterea tensiunii la motoare, constatăm că energia cinetică medie a rulmenților cu bile crește (postulatul 6).

Teoria moleculară cinetică poate fi utilizată pentru a explica fiecare dintre legile determinate experimental ale gazelor.

Legătura dintre P și n

Presiunea unui gaz rezultă din coliziunile dintre particulele de gaz și pereții containerului. De fiecare dată când o particulă de gaz lovește peretele, aceasta exercită o forță asupra peretelui. O creștere a numărului de particule de gaz din recipient mărește frecvența coliziunilor cu pereții și, prin urmare, presiunea gazului.

Legea amontonilor (PT)

Ultimul postulat al teoriei moleculare cinetice afirmă că energia cinetică medie a unei particule de gaz depinde doar de temperatura gazului. Astfel, energia cinetică medie a particulelor de gaz crește pe măsură ce gazul devine mai cald. Deoarece masa acestor particule este constantă, energia lor cinetică poate crește numai dacă viteza medie a particulelor crește. Cu cât aceste particule se mișcă mai repede când lovesc peretele, cu atât este mai mare forța pe care o exercită asupra peretelui. Pe măsură ce forța pe coliziune devine mai mare pe măsură ce temperatura crește, presiunea gazului trebuie să crească și ea.

Legea lui Boyle (P = 1/v)

Gazele pot fi comprimate deoarece majoritatea volumului unui gaz este spațiu gol. Dacă comprimăm un gaz fără a-i modifica temperatura, energia cinetică medie a particulelor de gaz rămâne aceeași. Nu există nicio modificare a vitezei cu care se mișcă particulele, dar containerul este mai mic. Astfel, particulele se deplasează de la un capăt la altul al containerului într-o perioadă mai scurtă de timp. Aceasta înseamnă că lovesc pereții mai des. Orice creștere a frecvenței coliziunilor cu pereții trebuie să ducă la o creștere a presiunii gazului. Astfel, presiunea unui gaz devine mai mare pe măsură ce volumul gazului devine mai mic.

Legea lui Charles (V T)

Energia cinetică medie a particulelor dintr-un gaz este proporțională cu temperatura gazului. Deoarece masa acestor particule este constantă, particulele trebuie să se miște mai repede pe măsură ce gazul devine mai cald. Dacă se mișcă mai repede, particulele vor exercita o forță mai mare asupra containerului de fiecare dată când lovesc pereții, ceea ce duce la o creștere a presiunii gazului. Dacă pereții containerului sunt flexibili, acesta se va extinde până când presiunea gazului va echilibra încă o dată presiunea atmosferei. Prin urmare, volumul gazului devine mai mare pe măsură ce temperatura gazului crește.

Ipoteza lui Avogadro (V N)

Pe măsură ce numărul particulelor de gaz crește, frecvența coliziunilor cu pereții containerului trebuie să crească. Acest lucru, la rândul său, duce la o creștere a presiunii gazului. Recipientele flexibile, cum ar fi un balon, se vor extinde până când presiunea gazului din interiorul balonului echilibrează din nou presiunea gazului din exterior. Astfel, volumul gazului este proporțional cu numărul de particule de gaz.

Imaginați-vă ce s-ar întâmpla dacă șase rulmenți cu bile de o dimensiune diferită ar fi adăugați la simulatorul de dinamică moleculară. Presiunea totală ar crește deoarece ar exista mai multe coliziuni cu pereții containerului. Dar presiunea datorată coliziunilor dintre rulmenții cu bile originale și pereții containerului ar rămâne aceeași. Există atât de mult spațiu gol în recipient, încât fiecare tip de rulment cu bile lovește pereții containerului la fel de des în amestec, ca atunci când era un singur tip de rulment cu bile pe placa de sticlă. Numărul total de coliziuni cu peretele din acest amestec este, prin urmare, egal cu suma coliziunilor care ar avea loc atunci când fiecare dimensiune a rulmentului cu bile este prezentă de la sine. Cu alte cuvinte, presiunea totală a unui amestec de gaze este egală cu suma presiunilor parțiale ale gazelor individuale.

Câteva dintre proprietățile fizice ale gazelor depind de identitatea gazului. Una dintre aceste proprietăți fizice poate fi văzută atunci când este studiată mișcarea gazelor.

În 1829 Thomas Graham a folosit un aparat similar cu cel prezentat în figura de mai jos pentru a studia difuzie de gaze viteza la care se amestecă două gaze. Acest aparat este format dintr-un tub de sticlă sigilat la un capăt cu tencuială care are găuri suficient de mari pentru a permite unui gaz să intre sau să iasă din tub. Când tubul este umplut cu gaz H2, nivelul apei din tub crește încet, deoarece moleculele H2 din interiorul tubului scapă prin găurile din tencuială mai rapid decât moleculele din aer pot pătrunde în tub. Studiind rata la care s-a schimbat nivelul apei din acest aparat, Graham a reușit să obțină date despre viteza la care diferite gaze se amestecau cu aerul.

Graham a descoperit că ratele la care gazele se difuzează sunt invers proporționale cu rădăcina pătrată a densităților lor.

Această relație a devenit în cele din urmă cunoscută sub numele de Legea difuziunii lui Graham.

Pentru a înțelege importanța acestei descoperiri, trebuie să ne amintim că volume egale de gaze diferite conțin același număr de particule. Ca rezultat, numărul de moli de gaz pe litru la o anumită temperatură și presiune este constant, ceea ce înseamnă că densitatea unui gaz este direct proporțională cu greutatea sa moleculară. Prin urmare, legea difuziunii lui Graham poate fi scrisă și după cum urmează.

Rezultate similare s-au obținut atunci când Graham a studiat rata de efuziune a unui gaz, care este rata la care gazul scapă printr-un orificiu în vid. Rata de revărsare a unui gaz este, de asemenea, invers proporțională cu rădăcina pătrată a densității sau a greutății moleculare a gazului.

Legea efuziunii lui Graham poate fi demonstrat cu aparatul din figura de mai jos. Un balon cu filtru cu pereți groși este evacuat cu o pompă de vid. O seringă este umplută cu 25 ml de gaz și timpul necesar pentru ca gazul să scape prin acul seringii în balonul filtrant evacuat se măsoară cu un cronometru.

După cum putem vedea când datele obținute în acest experiment sunt reprezentate grafic în figura de mai jos, timpul necesar pentru eșantioanele de 25 ml de diferite gaze pentru a scăpa în vid este proporțional cu rădăcina pătrată a greutății moleculare a gazului. Viteza la care se revarsă gazele este, prin urmare, invers proporțională cu rădăcina pătrată a greutății moleculare. Observațiile lui Graham despre viteza cu care gazele se difuzează (se amestecă) sau se revarsă (scapă printr-un orificiu) sugerează că particulele de gaz relativ ușoare, cum ar fi moleculele H2 sau atomii de He, se mișcă mai repede decât particulele de gaz relativ grele, cum ar fi moleculele de CO2 sau SO2.

Teoria moleculară cinetică poate fi utilizată pentru a explica rezultatele obținute de Graham atunci când a studiat difuzia și revărsarea gazelor. Cheia acestei explicații este ultimul postulat al teoriei cinetice, care presupune că temperatura unui sistem este proporțională cu energia cinetică medie a particulelor sale și nimic altceva. Cu alte cuvinte, temperatura unui sistem crește dacă și numai dacă există o creștere a energiei cinetice medii a particulelor sale.

Două gaze, cum ar fi H2 și O2, la aceeași temperatură, trebuie să aibă aceeași energie cinetică medie. Acest lucru poate fi reprezentat de următoarea ecuație.

Această ecuație poate fi simplificată prin înmulțirea ambelor părți cu două.

Apoi poate fi rearanjat pentru a da următoarele.

Luând rădăcina pătrată a ambelor părți ale acestei ecuații se obține o relație între raportul dintre vitezele la care se mișcă cele două gaze și rădăcina pătrată a raportului dintre greutățile lor moleculare.

Această ecuație este o formă modificată a legii lui Graham. Aceasta sugerează că viteza (sau viteza) la care se mișcă moleculele de gaz este invers proporțională cu rădăcina pătrată a greutăților lor moleculare.

Calculați viteza medie a unei molecule H2 la 0 ° C dacă viteza medie a unei molecule O2 la această temperatură este de 500 m/s.