Capacitate termică este capacitatea unui material de a absorbi căldura fără a reflecta direct totul ca o creștere a temperaturii. Ar trebui să citiți secțiunile despre căldură și temperatură ca fundal, iar secțiunea cu apă ar ajuta, de asemenea.
Deoarece căldura este adăugată în mod uniform pentru cantitățile similare de substanțe diferite, temperaturile lor pot crește la viteze diferite. De exemplu, metalele,
bun dirijori de căldură, arată că crește rapid temperatura când este încălzit. Este relativ ușor să încălziți un metal până când acesta luminează roșu. Pe de altă parte, apa poate absorbi multă căldură cu o creștere relativ mică a temperaturii. Izolator materiale (izolatori) sunt conductori de căldură foarte slabi și sunt folosiți pentru a izola materialele care trebuie păstrate la temperaturi diferite - cum ar fi interiorul casei dvs. din exterior.
Substanțele care absorb aceeași cantitate de căldură pot avea creșteri de temperatură diferite.
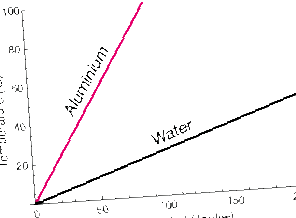
Acest grafic arată creșterea temperaturii pe măsură ce căldura este adăugată în același ritm la mase egale de aluminiu (Al) și apă (H2O). Temperatura apei crește mult mai încet decât cea a Al.
În metal, atomii de Al au doar energie cinetică de translație (deși această mișcare este cuplată puternic cu atomii vecini). Apa, pe de altă parte, se poate roti și vibra, de asemenea. Aceste grade de libertate de mișcare poate absorbi energia cinetică fără a o reflecta ca o creștere a temperaturii substanței.
Echiparea partiției Energiei
Majoritatea substanțelor respectă legea echiparea partiției energiei pe o gamă largă de temperaturi. Legea spune că energia tinde să fie distribuită în mod egal între toate gradele de libertate ale unei molecule și de translație, rotație și vibrație. Acest lucru are consecințe pentru substanțele cu mai mulți sau mai puțini atomi. În diagrama de mai jos, fiecare container reprezintă un grad de libertate. Situațiile pentru un 3-atom și un 10-atom
sunt prezentate molecule. Dacă se adaugă aceeași cantitate totală de energie termică la fiecare moleculă, molecula cu 3 atomi ajunge la mai multă energie în gradele sale de translație de libertate. Deoarece molecula cu 10 atomi are mai multe moduri de vibrație în care să stocheze energia cinetică, este mai puțin disponibil pentru a intra în modurile de translație și este cea mai mare parte a energiei de translație pe care o măsurăm ca temperatura.
Căldura specifică
Mai este încă un rafinament de făcut pentru a încălzi capacitatea. Evident, cantitatea de căldură necesară pentru creșterea temperaturii unei cantități mari de substanță este mai mare decât cantitatea necesară pentru o cantitate mică din aceeași substanță.
Pentru a controla cantitatea, în general măsurăm și raportăm capacitățile de căldură ca căldura specifică, capacitatea termică pe unitate de masă.
Căldurile specifice dintr-o mulțime de substanțe au fost măsurate în diferite condiții. Acestea sunt înscrise în cărți on-line.
În general, alegem unități de J/gram sau KJ/Kg. Căldura specifică a apei lichide este de 4.184 J/g, care este, de asemenea, 4.184 KJ/Kg. Caloria este o unitate de căldură definită ca cantitatea de căldură necesară pentru a crește temperatura de 1 cm 3 de apă cu 1ЛљC.
Căldura specifică
Căldura specifică este capacitatea de căldură pe unitate de masă.
Căldura specifică a apei este de 1 cal/gLљC = 4,184J/gLљC
Calculul modificărilor de căldură și temperatură
Căldura, q, necesare pentru ridicarea temperaturii unei mase, m, a unei substanțe cu o cantitate ΔT este
$$ q = mC \ Delta T = mC (T_f - T_i) $$
Unde C este căldura specifică și Tf și Tu sunt temperaturile finale și inițiale.
Panta unui grafic al temperaturii vs. căldura adăugată la o unitate de masă este de doar 1/C.
Folosind această formulă, este relativ ușor să calculați căldura adăugată, temperatura finală sau inițială sau căldura specifică în sine (așa se măsoară) dacă sunt cunoscute celelalte variabile.
Căldură adăugată pentru a obține o schimbare de temperatură
Căldura q adăugat sau evoluat pentru o schimbare de temperatură a unei mase m a unei substanțe cu căldură specifică C este
$$ q = mC \ Delta T = mC (T_f - T_i) $$
Unitățile de căldură specifice sunt de obicei J/mol · K (J · mol -1 K -1) sau J/g · K (J · g -1 · K · -1). Amintiți-vă că este OK să schimbați LљC cu K deoarece dimensiunea gradului Celsius și Kelvin sunt aceleași.
Exemplul 1
Calculați cantitatea de căldură (în Jouli) necesară pentru a schimba temperatura de 1 litru de apă (1 L = 1 Kg) de la 20ЛљC la 37ЛљC.
Capacitatea specifică de căldură (C) a apei este de 4.184 J/gЛљC (sau J/g · K - atâta timp cât lucrăm cu grade Celsius sau Kelvins, ΔT va fi la fel, deoarece dimensiunea celor două este aceeași. Fahrenheit este un grad mai mic). Ecuația de care avem nevoie este:
Conectând 1000 g pentru masa de 1 L de apă (gramul este definit ca masa de 1 ml de apă) și schimbarea temperaturii (37ЛљC - 20ЛљC), obținem:
$$ = (1000 \, g) \ left (4.185 \ frac \ right) (37 - 20) ЛљC $$
$$ = 71.128 \; J = \ bf 71 \; KJ $$
Când numărul de Jouli de energie depășește 1.000, în general exprimăm cantitatea în KiloJoules (KJ) pentru a simplifica numărul.
Exersează probleme
(Utilizați tabelul de mai jos pentru a căuta căderile specifice care lipsesc.)
| 1. | Câtă căldură (în Jouli) este nevoie pentru a crește temperatura de 100 g de H2O de la 22ЛљC la 98ЛљC? | Soluţie |
| 2. | Dacă este nevoie de 640 J de energie termică pentru a crește temperatura de 100 g dintr-o substanță cu 25ЛљC (fără a-și schimba faza), calculați căldura specifică a substanței. | Soluţie |
| 3. | Dacă se adaugă 80 J de căldură la 100 ml etanol [densitate (ρ) = 789 Kg · m -3] inițial la 10ЛљC, calculați temperatura finală a probei. | Soluţie |
Soluția problemei 1
Soluția problemei 2
Rearanjați ecuația căldurii pentru a rezolva pentru C:
$$ q = mC \ Delta T \; \ longrightarrow \; C = \ frac $$
Notă: atunci când calculați Δ T, este „OK pentru a utiliza fie grade Celsius, fie Kelvins, deoarece dimensiunea și, prin urmare, orice diferență, vor fi aceleași. Totuși, totul se destramă odată cu Fahrenheit.
Soluția problemei 3
Mai întâi rearanjați ecuația căldurii pentru a rezolva temperatura finală.
$$ \ begin q = mC \ Delta T \; & \ longrightarrow \; T_f - T_i = \ frac \\ & \ longrightarrow T_f = \ frac + T_i \ end $$
Acum calculați numărul de grame de etanol folosind densitatea și având grijă să urmați unitățile.
Căldura (entalpia) de schimbare de fază
. sau, dacă ne încălzim sau ne răcim printr-o temperatură de schimbare de fază
Schimbările de fază sunt o sursă mare sau o chiuvetă de căldură. Iată, de exemplu, curba de încălzire a apei.
Arată creșterea temperaturii pe măsură ce căldura este adăugată constant la apă. Iată ce se întâmplă în regiuni A-E:
A. Căldura este adăugată la apa solidă (gheață) sub 0ЛљC, iar temperatura acesteia crește constant.
B. Gheața solidă este topită în apă lichidă. În timpul adăugării căldurii latente de fuziune (ΔHf), dar se observă creșterea temperaturii, dar legăturile de hidrogen care țin gheața împreună se rup.
C. Căldura este adăugată la apa lichidă peste 0LљC, iar temperatura acesteia crește la o rată constantă până la punctul de fierbere la 100LљC.
D. Apa la 100LљC absoarbe o mare cantitate de energie termică la 100LљC deoarece suferă o tranziție de fază de la lichid la gaz. Aceasta este căldura latentă de vaporizare, ΔHv, energia necesară pentru ca apa să nu mai aibă o forță de coeziune.
E. În cele din urmă, apa gazoasă de peste 100LљC absoarbe căldura, crescându-i temperatura într-un ritm constant. Apa nu mai are tranziții de fază după aceasta.
Forțele intermoleculare atractive relativ mari dintre moleculele de apă conferă apei călduri foarte mari de fuziune și vaporizare. Comparativ cu majoritatea celorlalte substanțe, este nevoie de o cantitate mare de căldură pentru a topi gheața de apă și pentru a fierbe sau a evapora apa.
Entalpiile de fuziune și vaporizare sunt tabelate și pot fi căutate. Pagina Wikipedia a unui compus este de obicei un loc bun pentru a le găsi. Mai jos vom face un exemplu de calcul al căldurii pe măsură ce temperatura unei substanțe crește printr-o schimbare de fază.
Forțe coezive
Forțele coezive sunt forțe care țin împreună o substanță. Când apa lovește o suprafață cerată sau hidrofobă, aceasta formează picături mici ca sferă - „margele”. Aceste mărgele de apă minimizează contactul cu suprafața și aerul și maximizează contactul apei cu ea însăși. Apa lichidă este foarte coezivă. Formează legături intermitente, dar relativ puternice cu sine.
Alte substanțe precum CO2 nu au atracții intermoleculare atât de puternice și nu formează lichide sau solide decât dacă sunt foarte reci sau la o presiune foarte mare.
Căldura fazei de tranziție
Căldura absorbită sau eliberată la o tranziție de fază este calculată prin înmulțirea entalpiei de vaporizare, ΔHv, sau entalpia fuziunii, ΔHf după numărul de moli de substanță:
$$ \ begin q & = m \, \ Delta H_f \\ [5pt] q & = m \, \ Delta H_v \ end $$
Entalpia de fuziune este adesea numită „căldura latentă de fuziune”, iar entalpia de vaporizare este adesea numită „căldura latentă de vaporizare”.
Unitățile din ΔHf și ΔHv sunt Jouli/mol (J · mol -1) sau J/g (J · · g -1).
Exemplul 2
Calculați cantitatea de căldură necesară pentru a încălzi 18 g de gheață de la -20LљC la apă la 25LљC.
Soluţie: Este un faza de tranzitie de apă în acest interval de temperatură, deci această problemă va cuprinde trei pași:
- Ridicați temperatura gheții de la -20ЛљC la punctul de topire, 0ЛљC, folosind căldura specifică a gheții, C = 2.010 J · g -1 K -1 .
- Convertiți gheața în apă la 0ЛљC, utilizând entalpia molară de fuziune, ΔHf = 333,5 J · g -1 .
- Creșteți temperatura apei lichide de la 0LљC la 25LљC, folosind căldura specifică a apei, C = 4.184 J · · g -1 K -1 .
Iată calculele pentru fiecare dintre pașii noștri:
Pasul 1: Cantitatea de căldură necesară pentru a crește temperatura gheții (înainte ca aceasta să se topească) cu 20ЛљC este:
Rețineți că am convertit temperaturile Celsius în Kelvin.
Pasul 2: Cantitatea de căldură necesară pentru a topi 18 g de gheață este:
Pasul 3: Cantitatea de căldură necesară pentru creșterea temperaturii apei lichide cu 25ЛљC este:
Adunând toate aceste energii, obținem totalul, q = 2642 J,
Acum să comparăm acest lucru cu un calcul similar, dar de data aceasta vom încălzi apa lichidă prin punctul său de fierbere la un gaz.
Exemplul 3
Calculați căldura necesară pentru a crește temperatura de 18 g de apă lichidă la Ti = 80ЛљC la abur la 125ЛљC.
Soluţie: Aceasta este, de asemenea, o problemă în trei pași, dar de data aceasta vaporizăm apă. Iată pașii:
- Creșteți temperatura apei lichide de la 80LљC până la punctul de fierbere, 100LљC, folosind căldura specifică a apei, C = 4,184 J · g -1 K -1 .
- Convertiți apa în abur (apă gazoasă) la 100 ° C, utilizând entalpia molară de vaporizare, (Hf = 2258 J · g -1 .
- Creșteți temperatura aburului de la 100LљC la 125LљC, folosind căldura specifică a aburului, C = 2.010 J · g -1 K -1 .
Iată calculele pentru fiecare dintre pașii noștri:
Pasul 1: Cantitatea de căldură necesară pentru creșterea temperaturii apei (înainte ca aceasta să se vaporizeze) de la 80ЛљC la 100ЛљC este:
Pasul 2: Convertiți apa lichidă în abur la 100ЛЮC. Aici folosim căldura de vaporizare a apei:
Pasul 3: În cele din urmă, calculăm cantitatea de căldură necesară pentru a modifica temperatura celor 80 g de abur de la 100ЛљC la 125ЛљC:
Aproape acolo. Ultimul pas este să adăugați toate aceste energii împreună:
Observați că cea mai mare contribuție la această energie, de departe, este evaporarea apei - schimbarea acesteia din lichid în gaz. Acest proces necesită o cantitate extraordinară de energie și că energia reprezintă cantitatea mare de energie necesară pentru a fierbe apa pentru a produce abur în instalațiile electrice de toate tipurile (inclusiv nucleare) și pentru mijloacele eficiente pe care oamenii le au pentru a ne răci corpurile.: transpirație.
Exersează probleme
(Utilizați tabelul de mai jos pentru a căuta căldurile specifice care lipsesc; căldurile de fuziune sau vaporizare sunt date în probleme.)
| 1. | Câtă căldură (în Jouli) este nevoie pentru a schimba 120g de gheață la -10ЛљC în apă la 37ЛљC? (ΔHf = 334 KJ · Kg -1)? Rețineți că aceasta este o problemă în trei pași: încălziți mai întâi gheața la 0LљC, apoi convertiți toate cele 120g în lichid, apoi ridicați temperatura apei la 37LљC (temperatura corpului uman). | Soluţie |
| 2. | Câtă căldură este eliberată când 1 Kg de abur la 300LљC este răcit în lichid la 40LљC? (ΔHv = 2260 KJ · Kg -1) | Soluţie |
| 3. | Există suficientă căldură în 100 ml de apă la 25LљC pentru a topi complet 50g de gheață la 0LљC? (ΔHf = 334 KJ · Kg -1) | Soluţie |
Soluția problemei 1
Mai întâi calculați căldura necesară pentru a crește temperatura apei de la 10LљC la 0LљC
Acum convertiți 120 g de gheață la 0LљC în apă lichidă la 0LљC:
În cele din urmă, ridicați temperatura apei la 37ЛљC și adăugați energiile:
$$ q_ = 2352 \, J + 40080 \, J _ 18577 \, J = 61 \; KJ $$
Observați că cea mai mare parte a energiei intră în ruperea structurii obișnuite a rețelei cristaline a gheții (topirea ei).
Soluția problemei 2
Se răcește aburul de la 300LљC la 100LљC.
Convertiți aburul în lichid la 100LљC.
Se răcește lichidul de la 100LљC la 40LљC.
În cele din urmă, adăugați căldura pierdută.
$$ q_ = 416 + 2260 + 251 = 2.927 \; KJ = 2,9 \; MJ $$
Soluția problemei 3
În primul rând, de câtă căldură avem nevoie pentru a topi atâta gheață la 0LљC?
$$ q = m \ Delta H_f = (50 \, g) (334 \, J/g) = 16.700 \; J $$
Acum calculați cantitatea de căldură eliberată de 100 ml de apă pe măsură ce se răcește la 0LљC:
Nu există suficientă căldură în acea apă pentru a topi atâta gheață.
Călduri specifice ale compușilor selectați
| Gheață de apă (H2O) | 2.11 |
| Apă lichidă | Cel mai frecvent 4.184 |
| Gaz de apă | 2.08 |
| Aluminiu (i) (Al) | 0,897 |
| Cupru (cu) (Cu) | 0,385 |
| Fier (e) (Fe) | 0,450 |
| Plumb (i) (Pb) | 0,129 |
| Metanol (1) (CH3OH) | 2.14 |
| Etanol (1) (C2H5OH) | 2,44 |
| Etilen glicol (l) (C2O2H6) | 2.2 |
| Hidrogen (g) (H2) | 14.267 a celei mai frecvente |
| Benzen (l) (C6H6) | 1.750 este cel mai frecvent |
| lemn (tipic) | 1.674 e cel mai frecvent |
| sticla (tipic) | 0,867 |
Rafinare: Cp și Cv
Până acum, pentru a simplifica lucrurile, m-am referit la căldura specifică ca fiind C. Dar capacitatea de căldură (căldură specifică dacă este pe mol sau pe gram) se poate modifica în funcție de variabilele termodinamice ale presiunii sau temperaturii sunt menținute constante în timpul încălzirii sau răcirii.
În general, în laborator lucrăm la presiune constantă - presiune atmosferică, deci Cp este cea mai frecvent utilizată căldură specifică.
În sistemele menținute la volum constant, cum ar fi într-o butelie de gaz, unde presiunea se poate modifica, dar volumul nu, putem folosi capacitatea de căldură la volum constant, CV.
Capacități relative de căldură - Cp de apă este mare
Unul dintre cele mai interesante și importante lucruri despre apă este căldura specifică ridicată în comparație cu alte molecule de dimensiunea sa. Este anormal de mare și se consideră că această caracteristică este cuplată în câteva moduri la originea vieții pe Pământ. Unicitatea apei în acest sens este parțial motivul pentru care căutăm apă pe alte planete și luni atunci când căutăm semne de viață extraterestră.
Un exemplu de conservare a energiei
10 g de gheață la -10LљC se adaugă la 100 g de apă la 50LљC. Calculați temperatura finală a acestui amestec odată ce gheața s-a topit și temperatura s-a echilibrat. Nu presupuneți niciun schimb de căldură cu împrejurimile (condiții adiabatice).
Această problemă este rezolvată folosind principiul conservării energiei. Dacă nu se pierde căldură în împrejurimi și nimeni nu are voie să intre în sistem, atunci toată căldura utilizată pentru a topi gheața și a încălzi lichidul rezultat trebuie să provină din apa de 50LљC.
Căldura pierdută de apă = căldura câștigată de gheață
O problemă obișnuită cu rezolvarea unor astfel de probleme este contabilitatea - ținerea evidenței semnelor pentru pierderea de căldură și câștigul de căldură. Veți avea rezultate mai bune dacă lucrați astfel:
Căldura pierdută de apă este
$$ \ begin q & = m C \ Delta T \\ & = (100 \, g) \ left (4.184 \ frac \ right) (T_f - 50) ЛЮC \\ & = 418.4 \, T_f - 20.920 \ end $ $
unde Tf este temperatura finală necunoscută.
Căldura câștigată de gheață include căldura pentru a aduce temperatura solidului la 0ЛљC, căldura necesară pentru a o topi și căldura pentru a o aduce la temperatura finală, Tf.
Acum, dacă adăugăm căldura pierdută de apă la căldura câștigată de gheață și stabilim suma egală cu zero, obținem:
418,4 $ T_f - 20920 + 211 + 3340 + 41,84 T_f = 0 $$
Apoi ne adunăm ca niște termeni și rezolvăm temperatura finală:
$$ \ begin 460.24 \, T_f & = 20920 - 211 - 3340 \\ \ bf T_f & = 37,7 ЛљC \ end $$
Această temperatură are sens. Apa a fost răcită pe măsură ce topea gheața, dar nu prea mult, deoarece există de 10 ori mai multă apă în masă.
- Căldură indirectă Modul ușor de a face pește la grătar; Parteneriat pentru nutriția fructelor de mare
- Căldură - Energie regenerabilă 2019 - Analiză - IEA
- Căldură și fertilitate masculină WINFertilitate
- Câte calorii de căldură sunt necesare pentru a crește temperatura apei de la 10
- Gestionarea diabetului în CDC cu diabet termic