Luați în considerare un circuit pentru un sistem de alimentare cu curent alternativ monofazat, în care o sursă de tensiune alternativă de 120 volți și 60 Hz furnizează energie unei sarcini rezistive: (Figura de mai jos)
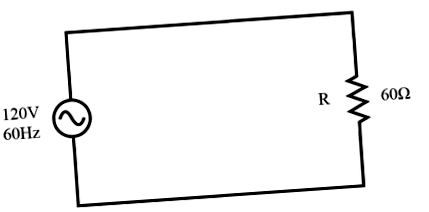
[latex] Z = 60 + j0 \ Omega \ textbf < or >60 \ Omega \ angle \ text< 0°>[/ latex]
În acest exemplu, curentul la încărcare ar fi de 2 amperi, RMS. Puterea disipată la sarcină ar fi de 240 wați. Deoarece această sarcină este pur rezistivă (fără reactanță), curentul este în fază cu tensiunea, iar calculele arată similar cu cel dintr-un circuit DC echivalent. Dacă ar fi să trasăm formele de undă de tensiune, curent și putere pentru acest circuit, ar arăta ca figura de mai jos.
Figura 7.1 Curentul este în fază cu tensiunea într-un circuit rezistiv.
Rețineți că forma de undă pentru putere este întotdeauna pozitivă, niciodată negativă pentru acest circuit rezistiv. Aceasta înseamnă că puterea este întotdeauna disipată de sarcina rezistivă și nu se întoarce niciodată la sursă, așa cum este cu sarcinile reactive. Dacă sursa ar fi un generator mecanic, ar fi nevoie de 240 de wați de energie mecanică (aproximativ 1/3 cai putere) pentru a roti arborele.
De asemenea, rețineți că forma de undă pentru putere nu este la aceeași frecvență ca tensiunea sau curentul! Mai degrabă, frecvența sa este dublă față de formele de undă de tensiune sau curent. Această frecvență diferită interzice exprimarea puterii noastre într-un circuit de curent alternativ utilizând aceeași notație complexă (dreptunghiulară sau polară) ca și cea utilizată pentru tensiune, curent și impedanță, deoarece această formă de simbolism matematic implică relații de fază neschimbate. Când frecvențele nu sunt aceleași, relațiile de fază se schimbă constant.
Oricât de ciudat ar părea, cel mai bun mod de a continua cu calculele puterii de curent alternativ este să folosiți notația scalară și să gestionați orice relație de fază relevantă cu trigonometria.
Circuit de curent alternativ cu o sarcină pur reactivă
Pentru comparație, să luăm în considerare un circuit simplu de curent alternativ cu o sarcină pur reactivă în figura de mai jos.
Circuit de curent alternativ cu o sarcină pur reactivă (inductivă).
[latex] X_L = 60.319 \ Omega [/ latex]
[latex] Z = 0 + j60.319 \ Omega \ text < or >60.319Ω \ angle \ text< 90°>[/ latex]
Figura 7.2 Puterea nu este disipată într-o sarcină pur reactivă. Deși este alternativ absorbit și returnat la sursă.
Rețineți că puterea alternează în mod egal între ciclurile pozitiv și negativ. (Figura de mai sus) Aceasta înseamnă că puterea este absorbită alternativ și returnată la sursă. Dacă sursa ar fi un generator mecanic, nu ar fi nevoie (practic) de energie mecanică netă pentru a roti arborele, deoarece sarcina nu ar folosi energie. Arborele generatorului ar fi ușor de rotit, iar inductorul nu s-ar încălzi ca un rezistor.
Circuit de curent alternativ cu o sarcină rezistivă și pur reactivă
Acum, să luăm în considerare un circuit de curent alternativ cu o sarcină constând atât din inductanță, cât și din rezistență în figura de mai jos.
circuit atât cu reactanță cât și rezistență.
[latex] X_L = 60.319 \ Omega [/ latex]
[latex] Z_L = 0 + j60.319 \ Omega [/ latex] sau [latex] 60.319 \ Omega \ angle 90 ° [/ latex]
[latex] Z_R = 60 + j0 \ Omega [/ latex] sau [latex] 60 \ Omega \ angle 0 ° [/ latex]
[latex] Z_> = 60+ j60.319 \ Omega [/ latex] sau [latex] 85.078 \ Omega \ angle 45.152 ° [/ latex]
La o frecvență de 60 Hz, cei 160 de milenirys de inductanță ne oferă 60.319 Ω de reactanță inductivă. Această reactanță se combină cu rezistența de 60 Ω pentru a forma o impedanță de încărcare totală de 60 + j60.319 Ω, sau 85.078 Ω ∠ 45.152 o. Dacă nu ne preocupă unghiurile de fază (care nu suntem în acest moment), putem calcula curentul în circuit luând magnitudinea polară a sursei de tensiune (120 volți) și împărțindu-l la magnitudinea polară a impedanței (85.078). Cu o tensiune de alimentare de 120 volți RMS, curentul nostru de încărcare este de 1.410 amperi. Aceasta este cifra pe care un ampermetru RMS ar indica-o dacă este conectată în serie cu rezistorul și inductorul.
Știm deja că componentele reactive disipă puterea zero, deoarece absorb în mod egal puterea și restituie puterea către restul circuitului. Prin urmare, orice reactanță inductivă în această sarcină va disipa, de asemenea, puterea zero. Singurul lucru care rămâne pentru a disipa puterea aici este porțiunea rezistivă a impedanței de încărcare. Dacă ne uităm la diagrama formei de undă a tensiunii, curentului și puterii totale pentru acest circuit, vedem cum funcționează această combinație în figura de mai jos.
Figura 7.3 Un circuit combinat rezistiv/reactiv disipează mai multă putere decât revine la sursă. Reactanța disipează nicio putere; totuși, rezistența o face.
La fel ca în cazul oricărui circuit reactiv, puterea alternează între valori pozitive și negative instantanee în timp. Într-un circuit pur reactiv, alternanța dintre puterea pozitivă și cea negativă este împărțită în mod egal, rezultând o disipare a puterii nete de zero. Cu toate acestea, în circuite cu rezistență și reactanță mixte ca aceasta, forma de undă a puterii va alterna în continuare între pozitiv și negativ, dar cantitatea de putere pozitivă va depăși cantitatea de putere negativă. Cu alte cuvinte, sarcina combinată inductivă/rezistivă va consuma mai multă energie decât se întoarce înapoi la sursă.
Privind diagrama formei de undă pentru putere, ar trebui să fie evident că unda petrece mai mult timp pe partea pozitivă a liniei medii decât pe cea negativă, indicând faptul că există mai multă putere absorbită de sarcină decât este returnată circuitului. Ce mică revenire a puterii care se produce se datorează reactanței; dezechilibrul puterii pozitive versus negative se datorează rezistenței deoarece disipă energia în afara circuitului (de obicei sub formă de căldură). Dacă sursa ar fi un generator mecanic, cantitatea de energie mecanică necesară pentru rotirea arborelui ar fi cantitatea de putere medie între ciclurile de putere pozitive și negative.
Reprezentarea matematică a puterii într-un circuit de curent alternativ este o provocare, deoarece unda de putere nu este la aceeași frecvență ca tensiunea sau curentul. Mai mult, unghiul de fază pentru putere înseamnă ceva destul de diferit de unghiul de fază pentru tensiune sau curent. În timp ce unghiul pentru tensiune sau curent reprezintă o schimbare relativă de sincronizare între două unde, unghiul de fază pentru putere reprezintă un raport între puterea disipată și puterea returnată. Datorită acestui mod în care puterea de curent alternativ diferă de tensiunea sau curentul de curent alternativ, este de fapt mai ușor să se ajungă la cifre pentru putere, calculând cu cantități scalare de tensiune, curent, rezistență și reactanță decât să încercați să o derivați din vector, sau cantități complexe de tensiune, curent și impedanță cu care am lucrat până acum.
- Într-un circuit pur rezistiv, toată puterea circuitului este disipată de rezistență (rezistențe). Tensiunea și curentul sunt în fază una cu cealaltă.
- Într-un circuit pur reactiv, nici o putere a circuitului nu este disipată de sarcină (sarcini). Mai degrabă, puterea este alternativ absorbită și returnată la sursa de curent alternativ. Tensiunea și curentul sunt defazate la 90 ° între ele.
- Într-un circuit format din rezistență și reactanță amestecate, va exista mai multă putere disipată de sarcină (sarcini) decât cea returnată, dar o anumită putere va fi cu siguranță disipată, iar unele vor fi doar absorbite și returnate. Tensiunea și curentul într-un astfel de circuit vor fi defazate cu o valoare undeva între 0 ° și 90 °.
Puterea reactivă
Știm că sarcinile reactive, cum ar fi inductoarele și condensatoarele disipă puterea zero, totuși faptul că scad tensiunea și trag curent oferă impresia înșelătoare că disipă puterea. Această „putere fantomă” se numește putere reactivă și este măsurată într-o unitate numită Volt-Amps-Reactive (VAR), mai degrabă decât în wați. Simbolul matematic pentru puterea reactivă este (din păcate) litera mare Q.
Puterea adevărată
Cantitatea reală de energie utilizată sau disipată într-un circuit se numește putere reală și este măsurată în wați (simbolizată cu litera mare P, ca întotdeauna).
Putere aparentă
Combinația dintre puterea reactivă și puterea adevărată se numește putere aparentă și este produsul tensiunii și curentului unui circuit, fără referire la unghiul de fază. Puterea aparentă este măsurată în unitatea Volt-Amps (VA) și este simbolizată cu litera mare S.
Se calculează puterea reactivă, adevărată sau aparentă
De regulă, adevărata putere este o funcție a elementelor disipative ale unui circuit, de obicei rezistențe (R). Puterea reactivă este o funcție a reactanței unui circuit (X). Puterea aparentă este o funcție a impedanței totale (Z) a unui circuit. Deoarece avem de-a face cu mărimi scalare pentru calcularea puterii, orice mărimi de pornire complexe, cum ar fi tensiunea, curentul și impedanța, trebuie să fie reprezentate de magnitudinile lor polare, nu de componente dreptunghiulare reale sau imaginare. De exemplu, dacă calculez adevărata putere din curent și rezistență, trebuie să folosesc magnitudinea polară pentru curent și nu doar porțiunea „reală” sau „imaginară” a curentului. Dacă calculez puterea aparentă din tensiune și impedanță, ambele aceste cantități anterior complexe trebuie reduse la magnitudinile lor polare pentru aritmetica scalară.
Ecuații folosind cantități scalare
Există mai multe ecuații de putere care leagă cele trei tipuri de putere de rezistență, reactanță și impedanță (toate folosind cantități scalare):
Puterea adevărată
[latex] \ begin \ tag & P = IECosθ \\ & P = I ^ 2R \\ & P = \ frac \ end [/ latex]
Măsurată în unități de Watts (w)
Puterea reactivă
Măsurat în unități de Volți-amperi-reactivi (VAR)
Putere aparentă
Măsurat în unități de Volți-amperi (VA)
Vă rugăm să rețineți că există două ecuații pentru calculul puterii reale și reactive. Există trei ecuații disponibile pentru calculul puterii aparente, P = IE fiind util numai în acest scop. Examinați următoarele circuite și vedeți cum se corelează aceste trei tipuri de putere: o sarcină pur rezistivă, o sarcină pur reactivă și o sarcină rezistivă/reactivă.
Numai încărcare rezistivă
Puterea adevărată, puterea reactivă și puterea aparentă pentru o sarcină pur rezistivă.
[latex] P = I ^ 2R = 0W [/ latex]
[latex] Q = I ^ 2X = 238,73 VAR [/ latex]
[latex] S = I ^ 2Z = 238,73 [/ latex]
Numai sarcină reactivă
[latex] Q = I ^ 2X = 238,73 VAR [/ latex]
Puterea adevărată, puterea reactivă și puterea aparentă pentru o sarcină pur rezistivă.
Sarcină rezistivă/reactivă
Puterea adevărată, puterea reactivă și puterea aparentă pentru o sarcină rezistivă/reactivă.
Triunghiul puterii
Aceste trei tipuri de putere - adevărată, reactivă și aparentă - se raportează între ele sub formă trigonometrică. Numim asta triunghiul puterii: (Figura de mai jos).
Figura 7.4 Triunghi de putere care leagă puterea aparentă de puterea reală și puterea reactivă.
Folosind legile trigonometriei, putem rezolva lungimea oricărei laturi (cantitatea oricărui tip de putere), având în vedere lungimile celorlalte două laturi sau lungimea unei laturi și un unghi.
- Puterea disipată de o sarcină este denumită putere adevărată. Puterea adevărată este simbolizată prin litera P și este măsurată în unitatea de wați (W).
- Puterea doar absorbită și returnată în sarcină datorită proprietăților sale reactive este denumită putere reactivă. Puterea reactivă este simbolizată prin litera Q și este măsurată în unitatea Volt-Amps-Reactive (VAR).
- Puterea totală într-un circuit de curent alternativ, atât disipată, cât și absorbită/returnată este denumită putere aparentă. Puterea aparentă este simbolizată prin litera S și este măsurată în unitatea de volt-amperi (VA).
- Aceste trei tipuri de putere sunt legate trigonometric între ele. Într-un triunghi dreptunghiular, P = lungimea adiacentă, Q = lungimea opusă și S = lungimea hipotenuzei. Unghiul opus este egal cu unghiul de fază al impedanței (Z) circuitului.
După cum sa menționat anterior, unghiul acestui „triunghi de putere” indică grafic raportul dintre cantitatea de putere disipată (sau consumată) și cantitatea de putere absorbită/returnată. De asemenea, se întâmplă să fie același unghi ca și cel al impedanței circuitului în formă polară. Atunci când este exprimat ca o fracțiune, acest raport între puterea reală și puterea aparentă se numește factorul de putere pentru acest circuit. Deoarece puterea adevărată și puterea aparentă formează laturile adiacente și respectiv hipotenuzele unui triunghi dreptunghiular, raportul factorului de putere este, de asemenea, egal cu cosinusul acelui unghi de fază. Folosind valori din ultimul exemplu de circuit:
- Corecție practică a factorului de putere Manual de electronică al factorului de putere
- Factor de putere (PF)
- Măsuri de siguranță pentru sursele de alimentare Precauții pentru sursele de alimentare OMRON Industrial Automation
- Max Factor - Mascara cu 2000 de calorii Recenzii beautyheaven
- Max Factor 2000 Calorie Curved Brush Volume & Curl Mascara - «Pensula curbată necesită unele abilități
