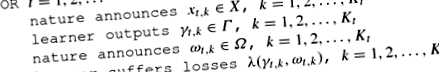Abstract

Această lucrare formulează un protocol pentru predicția pachetelor, care este un caz special de predicție on-line sub feedback întârziat. Conform protocolului de predicție a pachetelor, elevul trebuie să facă câteva predicții fără a vedea rezultatele respective și apoi rezultatele sunt dezvăluite dintr-o dată. Lucrarea dezvoltă teoria predicției cu sfaturi de specialitate pentru pachete prin generalizarea conceptului de mixabilitate. Propunem o serie de algoritmi de fuzionare pentru predicția pachetelor cu limite superioare strânse de pierderi de cazuri, similare cu cele pentru algoritmul de agregare al lui Vovk. Spre deosebire de algoritmii existenți pentru setările de feedback întârziat, algoritmii noștri nu depind de ordinea rezultatelor dintr-un pachet. Se efectuează experimente empirice privind seturile de date despre prețuri sportive și case, pentru a studia performanța noilor algoritmi și a le compara cu o metodă existentă.

Introducere

Această lucrare tratează protocolul de predicție on-line, în care un cursant trebuie să prezică rezultatele \ (\ omega _1, \ omega _2 \ ldots \) ​​care apar în succesiune. Elevul primește feedback pe parcurs.

În protocolul de predicție online de bază, pe pas t cursantul produce o predicție \ (\ gamma _t \) și apoi vede imediat rezultatul adevărat \ (\ omega _t \), care este feedback-ul. Calitatea predicției este evaluată printr-o funcție de pierdere \ (\ lambda (\ gamma, \ omega) \) care măsoară discrepanța dintre predicție și rezultat sau, în general vorbind, cuantificând efectul (advers) atunci când o predicție \ (\ gamma \) se confruntă cu rezultatul \ (\ omega \). Performanța cursantului este evaluată prin pierderea cumulată peste T încercări \ (\ sum _ ^ T \ lambda (\ gamma _t, \ omega _t) \) .

În această lucrare, ne preocupă problema predicției cu sfaturi de specialitate. Să presupunem că cursantul are acces la predicțiile unui număr de experți. Înainte ca elevul să facă o predicție, poate vedea predicțiile experților și scopul său este de a suferi pierderi apropiate de cea a celui mai bun expert retrospectiv.

Într-un protocol cu ​​feedback întârziat, poate exista o întârziere în obținerea rezultatelor adevărate \ (\ omega _t \). Este posibil ca elevul să trebuiască să facă câteva predicții înainte de a vedea efectiv rezultatele încercărilor din trecut. Vom lua în considerare un caz special al protocolului respectiv atunci când vor apărea rezultatele pachete: cursantul trebuie să facă câteva predicții, decât toate rezultatele sunt dezvăluite și din nou trebuie făcute câteva predicții.

O problemă care se potrivește în mod natural acestui cadru este asigurată de agregarea predicțiilor caselor de pariuri. Vovk și Zhdanov (2009) prezic rezultatele meciurilor sportive pe baza probabilităților calculate din cotele citate de casele de pariuri. Dacă meciurile apar una câte una, problema se potrivește în mod natural cu predicția de bază cu cadrul de sfaturi ale experților. Cu toate acestea, este obișnuit (de exemplu, în Premier League engleză) ca câteva meciuri să aibă loc în aceeași zi. Ar fi firesc să încerci și să previzi toate rezultatele în prealabil. Toate meciurile din aceeași zi pot fi tratate ca un pachet în cadrul nostru.

Dezvoltăm o teorie a predicției cu sfaturi de specialitate pentru pachete prin extinderea algoritmului de agregare (AA) introdus de Vovk (1990, 1998). În sectă. 2.2 și Anexa A, analizăm teoria existentă a AA pentru prezicerea rezultatelor unice (în terminologia noastră, pachete de mărimea unu). Teoria se bazează pe conceptul de mixabilitate a mediilor de predicție numite jocuri. În sectă. 3, dezvoltăm teoria mixabilității pentru jocuri cu pachete de rezultate. Teorema 1 arată că un joc care implică pachete de K rezultatele au același profil de constante de mixabilitate ca și jocul original cu rezultate unice, dar rata de învățare se împarte la K. Această observație ne permite să gestionăm pachete de dimensiuni constante. Cu toate acestea, după cum sa discutat mai sus, în cazuri cu adevărat interesante, dimensiunea ambalajului variază în funcție de timp și, prin urmare, amestecabilitatea mediului variază de la un pas la altul. Această problemă poate fi abordată în moduri diferite, rezultând algoritmi diferiți cu limite de performanță diferite. În sectă. 4, introducem trei Algoritmi de agregare pentru predicția pachetelor, AAP-max, AAP-incremental și AAP-curent și obțin limite superioare în cel mai rău caz pentru pierderea lor cumulativă.

Teoria generală a AA (Vovk 1998) ne permite să arătăm în Sect. 5 că într-un anumit sens limitele noastre sunt optime. În sectă. 5.1, oferim o derivare independentă a unei limite inferioare pentru cadrul mix-loss al lui Adamskiy și colab. (2016). Cu toate acestea, problema optimității pentru pachete este departe de a fi complet rezolvată și necesită investigații suplimentare.

După cum sa menționat anterior, problema predicției pachetelor poate fi considerată ca un caz special al problemei de feedback întârziat. Această problemă a fost studiată în principal în cadrul optimizării convexe online (Zinkevich 2003; Joulani și colab. 2013; Quanrud și Khashabi 2015). Terminologia și abordarea optimizării convexe online sunt diferite de ale noastre, care se întorc la Littlestone și Warmuth (1994) și au fost chestionate de Cesa-Bianchi și Lugosi (2006).

Problema predicției cu sfaturi de experți pentru feedback întârziat poate fi rezolvată prin rularea copiilor paralele ale algoritmilor care prezic rezultate individuale. În sectă. 2.3, descriem algoritmul Copii paralele, care este în esență BOLD al lui Joulani și colab. (2013) folosind algoritmul de agregare ca algoritm de bază pentru rezultate unice. Teoria algoritmului de agregare implică cel mai rău caz superior la pierderea copiilor paralele. Vedem că termenul de regret se înmulțește cu întârzierea maximă sau dimensiunea ambalajului ca în literatura existentă (Joulani și colab. 2013; Weinberger și Ordentlich 2002).

Limitele pe care le obținem pentru noii noștri algoritmi sunt aceleași (AAP-max și AAP-incremental) sau incompatibile (AAP-curent) cu limitele pentru Copii paralele. Discutăm limitele în sectă. 5 și apoi în sectă. 6 efectuați o comparație empirică a performanței algoritmilor.

Pentru experimente, prezicem rezultatele meciurilor sportive pe baza cotelor caselor de pariuri și stabilim prețurile caselor pe baza descrierilor caselor. Seturile de date sportive includ meciuri de fotbal, care conțin în mod natural pachete, și meciuri de tenis, unde introducem pachete în mod artificial în două moduri diferite. Seturile de date privind prețul locuințelor conțin înregistrări ale tranzacțiilor imobiliare din Ames în SUA și zona Londrei. Seturile de date înregistrează doar luna unei tranzacții, deci sunt organizate în mod natural în pachete. Experimentele privind prețul locuințelor urmează abordarea lui Kalnishkan și colab. (2015): predicția cu sfaturi de experți poate fi utilizată pentru a găsi informații relevante din trecut. Predictorii instruiți pe diferite secțiuni ale datelor anterioare pot fi combinate în modul on-line, astfel încât datele anterioare relevante să fie utilizate pentru predicție.

Performanța algoritmului Copii paralele depinde de ordinea rezultatelor din pachete, în timp ce algoritmii noștri sunt independenți de ordine. Comparăm pierderea cumulativă a algoritmilor noștri cu pierderea copiilor paralele mediată peste permutările aleatorii din pachete. Concluzionăm că, în timp ce copiile paralele pot funcționa foarte bine, mai ales dacă ordinea rezultatelor din pachete oferă informații utile, pierderea algoritmilor noștri este întotdeauna aproape de pierderea medie a copiilor paralele și unii algoritmi depășesc media.

Apoi, comparăm algoritmii noștri, concluzionând că AAP-max este cel mai rău și curentul AAP depășește AAP-incremental dacă raportul dintre dimensiunea maximă și cea minimă a pachetului este mic.

Preliminarii și antecedente

În această secțiune introducem cadrul de predicție a pachetelor și analizăm conexiunile cu literatura de specialitate.

Protocoale pentru predicția pachetelor

Un joc \ (\ mathfrak = \ langle \ varOmega, \ varGamma, \ lambda \ rangle \) este un triplu al unui spațiul de rezultat \ (\ varOmega \), spațiul de predicție \ (\ varGamma \) și funcția de pierdere \ (\ lambda: \ varGamma \ times \ varOmega \ rightarrow [0, + \, \ infty] \) .

Rezultatele \ (\ omega _1, \ omega _2, \ ldots \ in \ varOmega \) apar succesiv. A student sau strategia de predicție scoate predicții \ (\ gamma _1, \ gamma _2, \ ldots \ in \ varGamma \) înainte de a vedea rezultatele respective. Elevul poate avea acces la unele informații secundare; vom spune că elevul vede semnale \ (x_t \) provenind de la un spațiu semnalX.

În protocolul clasic, elevul face o predicție (posibil la utilizarea unui semnal) și apoi rezultatul este imediat dezvăluit. În această lucrare luăm în considerare o extindere a acestui protocol și permitem ca rezultatele să intre pachete de dimensiuni posibil diferite. Elevul trebuie să producă un pachet de predicții înainte de a vedea rezultatele adevărate. Următorul protocol rezumă cadrul.

Protocolul 1

(Predicția pachetelor)

predicția

La fiecare proces t elevul trebuie să facă predicții \ (K_t \) mai degrabă decât una. Vom vorbi despre un pachet de predicții ale cursantului \ (\ gamma _ \ in \ varGamma \), \ (k = 1,2, \ ldots, K_t \), un pachet de rezultate \ (\ omega _ \ in \ varOmega \), \ (k = 1,2, \ ldots, K_t \) etc.

În această lucrare, presupunem un mediu de informare complet. Cursantul știe \ (\ varOmega \), \ (\ varGamma \) și \ (\ lambda \). Vede toate \ (\ omega _ \) pe măsură ce devin disponibile. Pe de altă parte, nu facem ipoteze cu privire la mecanismul care generează \ (\ omega _ \) și vom fi interesați de cele mai nefavorabile garanții pentru pierdere. Rezultatele nu trebuie să satisfacă ipoteze probabiliste precum i.i.d. și se pot comporta cu rea intenție.

Acum, să fim \ (\ mathcal_1, \ mathcal_2, \ ldots, \ mathcal_N \) cursanți care lucrează conform Protocolului 1. Ne vom referi la acești cursanți ca experți. Să presupunem că la fiecare rând, predicțiile lor sunt puse la dispoziția unui cursant \ (\ mathcal \) ca un tip special de informații secundare. Cursantul lucrează apoi în conformitate cu următorul protocol.

Protocolul 2

(Predicția pachetelor cu sfaturi de specialitate)

Scopul cursantului în această configurație este de a suferi o pierdere apropiată de cel mai bun expert în retrospectivă (în orice sens formal care poate fi atins). Căutăm strategii de fuziune pentru cursant asigurându-se că elevul obține pierderi cumulative scăzute în comparație cu experții; vom vedea că se poate cuantifica pierderea cumulativă în diferite moduri.

Strategiile de fuzionare care ne interesează sunt calculabile într-un sens natural; nu vom face însă afirmații exacte despre calculabilitate. Nu impunem restricții experților. În cele ce urmează, cititorul poate înlocui clauza „pentru toate predicțiile” (\ gamma _ (i) \) care apare în Protocolul 2 ”pentru clauza mai intuitivă„ pentru toți experții ”.

Pot exista variații subtile ale acestui protocol. În loc să obțină toate predicțiile \ (K_t \) de la fiecare expert simultan, cursantul poate obține predicții pentru fiecare rezultat unul câte unul și le face propriile înainte de a vedea următorul set de predicții ale experților. Pentru majoritatea analizelor noastre acest lucru nu contează, așa cum vom vedea mai târziu. Este posibil ca cursantul să fie nevoit să lucreze la fiecare „pachet” de predicții ale experților în mod secvențial, fără să știe măcar mărimea acestuia în prealabil. Singurul lucru care contează este că rezultatele vin dintr-o singură dată după ce cursantul a terminat de prezis pachetul.

Pachete de mărimea unu

Pentru pachetele de mărimea 1 (\ (K_t = 1 \), \ (t = 1,2, \ ldots \)), Algoritmul de agregare (AA) de Vovk (1990, 1998) rezolvă problema predicției cu sfaturi de specialitate în un sens foarte general.

Algoritmul se bazează pe noțiunea de mixabilitate.

Luați în considerare un joc \ (\ mathfrak = \ langle \ varOmega, \ varGamma, \ lambda \ rangle \). O constantă \ (C> 0 \) este admisibil Pentru o rata de învățare \ (\ eta> 0 \) dacă pentru fiecare \ (N = 1,2, \ ldots \), fiecare set de predicții \ (\ gamma (1), \ gamma (2), \ ldots, \ gamma (N) \) și fiecare distribuție \ (p (1), p (2), \ ldots, p (N) \) (astfel încât \ (p (i) \ ge 0 \) și \ (\ sum _ ^ Np i ) = 1 \)) există \ (\ gamma \ in \ varGamma \) care asigură pentru toate rezultatele \ (\ omega \ in \ varOmega \) inegalitatea

constanta de mixabilitate \ (C_ \ eta \) este cel mai mic dintre toate \ (C> 0 \) admisibil pentru \ (\ eta \). Acest minim este de obicei atins. De exemplu, se realizează pentru toți \ (\ eta> 0 \) ori de câte ori \ (\ varGamma \) este compact și \ (e ^ \) este continuu Nota de subsol 1 în \ (\ gamma \) .

Algoritmul de agregare are o rată de învățare \ (\ eta> 0 \), o constantă C admisibil pentru \ (\ mathfrak \) cu \ (\ eta \) și o distribuție anterioară \ (p (1), p (2), \ ldots, p (N) \) \ (p (i) \ ge 0 \) și \ (\ sum _ ^ Np (i) = 1 \)) pe experți \ (\ mathcal_1, \ mathcal_2, \ ldots, \ mathcal_N \) .

Folosim notația

pentru pierderea cumulativă a unui cursant și a experților (deoarece dimensiunea ambalajului este întotdeauna 1, omitem al doilea index k și scrieți, spuneți, \ (\ omega _t \) în loc de \ (\ omega _ \)). Următoarea propoziție oferă o limită superioară a pierderii cursantului.

Propunerea 1

(Vovk 1990, 1998) Let C să fie admisibil pentru \ (\ eta> 0 \). Apoi pentru fiecare \ (N = 1,2, \ ldots \), pierderea unui cursant \ (\ mathcal \) folosind AA cu \ (\ eta \) și o distribuție anterioară \ (p (1), p 2 ), \ ldots, p (N) \) satisface

pentru fiecare expert \ (\ mathcal_i \), \ (i = 1,2, \ ldots, N \), toate orizonturile de timp \ (T = 1,2, \ ldots \) ​​și toate rezultatele realizate de natură. \ (\ pătrat \)

Pseudocodul algoritmului de agregare și dovada propunerii sunt date în apendicele A.

Alegerea unei anumite rate de învățare depinde de mărimea constantelor de mixabilitate. Pentru unele jocuri avem alegeri naturale optime. De exemplu, luați în considerare jocul general de pierdere pătrată cu \ (\ varOmega = \ varGamma = [A, B] \) și \ (\ lambda (\ gamma, \ omega) = (\ gamma - \ omega) ^ 2 \) utilizate pentru experimentele din această lucrare. Este una dintre așa-numitele mixabil jocuri cu C realizarea 1. Alegerea naturală a \ (\ eta \) este atunci valoarea maximă astfel încât \ (C_ \ eta = 1 \); minimizează al doilea termen din partea dreaptă a (2). Astfel de \ (\ eta \) este dat de \ (\ eta _0 = 2/(B-A) ^ 2 \); se poate adapta cu ușurință la interval [A, B] derivarea lui Vovk (2001) pentru intervalul \ ([- \, Y, Y] \) .

Observația 1

Pentru jocul cu pierderi pătrate generale, dacă se utilizează rata de învățare \ (\ eta _0 \), se poate găsi o valoare de \ (\ gamma \) care să satisfacă (1) pentru toate \ \ \ omega \ din [A, B] \) folosind un explicit funcția de substituție

după Vovk (2001). Acest lucru face ca algoritmul de agregare pentru jocul general de pierdere pătrată să fie eficient.

Pentru jocurile care nu se pot amesteca (cum ar fi jocul de pierdere absolută cu \ (\ lambda (\ gamma, \ omega) = | \ gamma - \ omega | \)), legat (2) oferă un compromis. Optimizarea legăturii este o sarcină mai dificilă și poate necesita presupuneri privind comportamentul experților sau orizontul de timp T.

Importanța AA rezultă din rezultatele lui Vovk (1998). Sub unele ipoteze ușoare de regularitate asupra jocului și presupunând distribuția inițială uniformă, se poate arăta că constantele inegalității (2) sunt optime. Dacă orice strategie de fuziune realizează garanția (cu \ (A> 0 \))

pentru toți experții \ (\ mathcal_1, \ mathcal_2, \ ldots, \ mathcal_N \), \ (N = 1,2, \ ldots \), orizonturi de timp T, și toate rezultatele, apoi AA cu distribuția anterioară uniformă \ (p (i) = 1/N \) și unele \ (\ eta> 0 \) oferă garanția cu aceeași sau mai mică C și A. Discutăm acest rezultat mai detaliat în Anexa A.

Abordarea întârziată a feedback-ului

Protocolul de predicție cu pachetele pe care le descriem poate fi considerat ca un caz special al setărilor de feedback întârziat studiate de Joulani și colab. (2013).

În predicția întârziată a feedbackului cu protocolul de sfaturi ale experților, la fiecare pas, cursantul primește doar o rundă de predicții de la fiecare expert și trebuie să-și producă propriile sale. Cu toate acestea, rezultatul corespunzător acestor predicții poate deveni disponibil mai târziu. Dacă este dezvăluit în același proces ca în Sect. 2.2, spunem că întârzierea este una. Dacă este dezvăluit în următorul proces, întârzierea este egală cu două etc. Predicția pachetelor de dimensiuni care nu depășesc K poate fi considerat ca o predicție cu întârzieri care nu depășesc K.

Algoritmul BOLD (Joulani și colab. 2013) pentru acest protocol funcționează după cum urmează. Luați un algoritm care lucrează cu întârzieri de 1 (sau pachete de dimensiunea 1); îl vom numi algoritmul de bază. Pentru a îmbina predicțiile experților, vom rula mai multe copii ale algoritmului de bază. Sunt independenți în sensul că nu împărtășesc informații. Fiecare copie va primi în mod repetat predicțiile experților pentru fuziune, va afișa o predicție și apoi va aștepta rezultatul corespunzător predicției. În fiecare moment, o copie a algoritmului de bază fie cunoaște toate rezultatele pentru predicțiile pe care le-a făcut, fie așteaptă rezultatul corespunzător ultimei predicții. În primul caz spunem că copia este gata (pentru a îmbina predicțiile mai multor experți) și în cazul ulterior spunem că copia este blocată (și nu poate fuziona).

La fiecare proces, când sosește o nouă rundă de predicții ale experților, alegem un algoritm gata (să zicem, unul cu cel mai mic număr) și îi oferim predicțiile experților. Produce o predicție, pe care o transmitem, iar algoritmul devine blocat până la sosirea rezultatului testului respectiv. Dacă toți algoritmii sunt în prezent blocați, începem o nouă copie a algoritmului de bază.

Să presupunem că jucăm un joc \ (\ mathfrak \) și C este admisibil pentru \ (\ mathfrak \) cu o rată de învățare \ (\ eta \). Pentru algoritmul de bază luați AA cu C, \ (\ eta \) și greutăți inițiale \ (p (1), p (2), \ ldots, p (N) \). Dacă întârzierea nu depășește niciodată D, nu avem nevoie niciodată de mai mult decât D algoritmi din matrice și fiecare dintre aceștia suferă pierderi satisfăcând Propoziția 1. Sumând limitele, obținem că pierderea lui \ (\ mathcal \) folosind această strategie satisface

pentru fiecare expert \ (\ mathcal_i \), unde suma din \ (>> _ T \) este preluată de toate rezultatele dezvăluite înainte de pasul \ (T + 1 \). Valoarea a D nu trebuie să fie cunoscut în prealabil; putem întotdeauna extinde matricea pe măsură ce întârzierea crește. Ne vom referi la combinația între BOLD și AA în modul de mai sus ca fiind Copii paralele algoritm.

Pentru Protocolul 2 putem defini pierderea cumulativă simplă