Săptămâna aceasta vom analiza două variante ale modelelor ARIMA - modele cu memorie lungă (diferențe fracționare) și modele de prag (modele de comutare de regim).

Obiective

  • Identificați și interpretați modele simple diferențiate fracțional
  • Recunoașteți când trebuie să luați primele diferențe vs. diferențe fracționare
  • Identificați și interpretați modelele ARFIMA
  • Aplicați modele diferite în două intervale ale unei serii temporale

Secțiunea 5.1 din Shumway și Stoffer oferă o scurtă prezentare generală a modelelor „ARMA cu memorie lungă”. Acest tip de model poate fi folosit când ACF-ul seriei se reduce încet la 0.

Soluția obișnuită în această situație este explorarea primelor diferențe ale seriei. Adesea, datele pentru care o primă diferență este reușită vor avea de obicei o autocorelare cu primul decalaj destul de apropiată de 1.

\ (x_t - x_ \) = termeni AR și MA.

Acest lucru poate fi rescris ca

\ (x_t = x_ + \) Termeni AR și MA.

În această formulare avem un termen AR de prim lag cu un coeficient egal cu 1. Acest lucru creează o autocorelație de prim ordin pentru seria originală apropiată de 1.

Cu toate acestea, în unele cazuri, putem vedea un model persistent de corelații diferite de zero, care începe cu o corelație de întârziere care nu este aproape de 1. În aceste cazuri, modelele care încorporează „diferențierea fracțională” pot fi utile. Un model simplu care utilizează diferențierea fracțională este

unde d este o valoare astfel încât | d | arfima poate fi folosit pentru a face acest lucru. Din nou, o indicație că acest model ar putea fi util este un eșantion de ACF încetinit lent, fără autocorelații deosebit de mari.

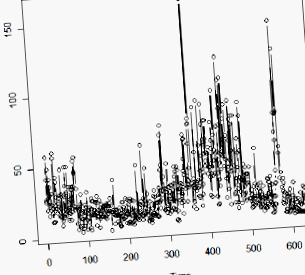
Exemplul 5.1 din text analizează un model diferențiat fracțional pentru o serie de valori n = 634 (anuale) ale unei măsurători geologice numite varve. Acesta este un strat sedimentar de nisip și nămol lăsat de topirea ghețarilor. Urmează o serie de date cronologice.

lecția

Datorită perioadei de variabilitate mai extremă, autorii sugerează analizarea logaritmului datelor. (Acest lucru ar putea stabiliza varianța.)

Urmează un complot al seriei transformate în jurnal:

Eșantionul ACF al datelor transformate în jurnal arată un model persistent de valori moderat ridicate. Iată atât ACF, cât și PACF. În capitolul 3 al textului, autorii folosesc prima diferențiere și explorează meritele relative ale modelelor ARIMA (0,1,1) și ARIMA (1,1,1) pentru aceste date. În secțiunea 5.1, autorii explorează un model diferențiat.

Pachetul arfima oferă o estimare pentru fracțiunea de diferențiere a \ (\ widehat = 0.373 \). Astfel, modelul estimat este \ (1-B) ^ x_t = w_t \) unde \ (x_t \) este seria centrală de jurnale transformate în jurnal.

Acest model oferă o potrivire bună a datelor, după cum reiese din următoarele ACF și PACF ale reziduurilor.

Generalizări

Modelul poate fi extins pentru a include termeni AR și MA, precum și diferența fracțională. Aceste modele se numesc modele ARFIMA. Pentru a identifica un model ARFIMA, folosim mai întâi modelul diferenței fracționale simple \ ((1-B) ^ dx_t = w_t \) și apoi explorăm ACF și PACF ale reziduurilor din acest model. Acest lucru este analog cu explorarea ACF și PACF a primelor diferențe atunci când efectuăm pașii obișnuiți pentru datele non-staționare. Pachetul arfima poate fi utilizat pentru a se potrivi modelelor generale ARFIMA.

Dificultate de interpretare

Principala dificultate este că o diferență fracțională este dificil de interpretat. Practic este un dispozitiv matematic care este folosit pentru a extinde un model într-un AR de mare ordin cu autocorelații care se potrivesc cu modelul persistent de „memorie lungă” din ACF din serie.

R R Cod pentru exemplul 5.1

Pentru a rula următorul cod, trebuie să instalați pachetul arfima; acest lucru este puternic încurajat de pachetul fracdiff acoperit în text (http://www.stat.pitt.edu/stoffer/tsa4/Rexamples.htm). Odată ce pachetul este instalat pe sistemul dvs., puteți sări peste etapa de instalare și să utilizați biblioteca (arfima) la fel ca și noi pentru biblioteca astsa.

Modelele prag sunt utilizate în mai multe domenii diferite ale statisticii, nu doar în serii cronologice. Ideea generală este că un proces se poate comporta diferit atunci când valorile unei variabile depășesc un anumit prag. Adică, se poate aplica un model diferit atunci când valorile sunt mai mari decât un prag decât atunci când sunt sub prag. În aplicațiile de toxicologie a medicamentelor, de exemplu, este posibil ca toate dozele sub o cantitate prag să fie sigure, în timp ce există o toxicitate crescândă, deoarece doza este crescută peste cantitatea prag. Sau, într-un studiu al abundenței populației de animale, populația poate crește încet până la o dimensiune prag, dar apoi poate scădea rapid (datorită hranei limitate) odată ce populația depășește o anumită dimensiune.

Modelele prag sunt un caz special al modelelor de comutare de regim (RSM). În modelarea RSM, diferite modele se aplică diferitelor intervale de valori ale unor variabile cheie.

Secțiunea 5.4 din textul nostru discută modelele autoregresive de prag (TAR) pentru serii temporale univariate. Într-un model TAR, modelele AR sunt estimate separat în două sau mai multe intervale de valori definite de variabila dependentă. Aceste modele AR pot fi sau nu de același ordin. Pentru comoditate, se presupune adesea că sunt de același ordin.

Textul consideră doar o singură valoare de prag, astfel încât vor exista două modele AR separate - unul pentru valorile care depășesc pragul și unul pentru valorile care nu. Dificultățile determină necesitatea unui model TAR, valoarea pragului de utilizat și ordinea (modelele) modelelor AR. O caracteristică pentru datele pe care un model TAR le poate funcționa este aceea că ratele de creștere și/sau scădere pot diferi atunci când valorile sunt peste un anumit nivel decât atunci când valorile sunt sub acel nivel.

Estimarea nivelului pragului este mai mult sau mai puțin subiectivă. Mulți analiști explorează mai multe niveluri de prag diferite, în încercarea de a oferi o potrivire bună a datelor (măsurate prin valorile MSE și caracteristicile generale ale reziduurilor). Ordinea (modelele) modelului (modelelor) AR poate fi, de asemenea, o expediție de încercare și eroare, mai ales atunci când modelul inerent pentru date poate să nu fie un AR. În general, analiștii încep cu ceea ce cred că ar putea fi o ordine mai mare decât este necesar și apoi reduc ordinea după cum este necesar.

Secțiunea 5.4 din text acoperă modelele de prag și include un exemplu frumos. În această lecție, vom discuta exemplul și vom furniza codul R. Seria pentru exemplu este rata lunară a deceselor cauzate de gripă în Statele Unite timp de 11 ani (n = 132). Datorită naturii epidemice a gripei, comportamentul seriei este destul de diferit atunci când ratele depășesc o anumită valoare prag decât atunci când este sub valoarea.

Primul pas (întotdeauna) este reprezentarea grafică a datelor. Urmează graficul seriei temporale a datelor.

În concordanță cu datele originale, observăm creșteri și scăderi accentuate în anumite perioade. După unele experimente, autorii au decis să utilizeze modele AR (4) separate pentru două regiuni: date după o primă diferență mai mare sau egală cu 0,05 și date după o primă diferență mai mică decât 0,05. Modelul se potrivește bine, ca dovadă a următoarelor grafice - ACF și PACF a reziduurilor și un grafic care compară prima diferență reală cu primele diferențe prevăzute. În graficul care compară valorile reale și cele prezise, ​​valorile prezise sunt de-a lungul liniei punctate roșii.

R R Cod pentru exemplu

Urmează codul R pentru exemplu. În cadrul comenzii ts.intersect comenzile lag (,) creează întârzieri și matricea care este afișată nu va conține rânduri cu valori lipsă. În cod, facem o potrivire de regresie a unui model AR (4) pentru toate datele pentru a seta variabilele care vor fi utilizate în regresiile regimului separat.

Pachetul tsDyn din R a simplificat acest cod într-o mână de pași:

Dacă nu oferim un prag pentru opțiunea a, setarea caută peste o grilă pentru a alege un prag (.036):